List of probability distributions > bimodal distribution
Bimodal Distribution: Two Peaks.
A bimodal distribution has two modes (peaks) that may or may not be symmetric .
Most probability distributions have one peak, which happens around the mean or median [2]. For example, a bell curve typically shows concentration of observations, typically around the central mean. However, a bimodal distribution has two distinct peaks – showing that data points are distributed across two separate values.
A mode indicates there is a single most common number within a set of data points, the “mode” in a bimodal distribution identifies two local maximums — where values stop trending up and start trending down. The mean and median lie between the two peaks and are not near either one [2].
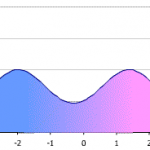
The “bi” in bimodal distribution comes from the Latin bis, which means two. “Modal” refers to the peaks.
Q. What does a Bimodal Distribution tell you?
You’ve got two peaks of data, which usually indicates you’ve got two different groups. For example, exam scores tend to be normally distributed with a single peak. However, grades sometimes fall into a bimodal distribution with a lot of students getting A grades and a lot getting F grades. This can tell you that you are looking at two different groups of students. It could be that one group is underprepared for the class (perhaps because of a lack of previous classes). The other group may have overprepared.
A bimodal distribution might result from a natural process such as the breakup of large particles, multiple sources of particles or variable growth mechanisms in a system [3]. In climatology, the Lifetime Maximum Intensity (LMI) distribution of tropical cyclones (defined as the peak one-minute maximum sustained wind achieved by a tropical cyclone during its lifetime) is bimodal, which means that major storms are not very rare compared to less intense storms [4] — although there is no consensus on why this bimodality occurs. [5].
Two peaks could also indicate your data is sinusoidal. If you suspect your data might be following a wave-like pattern, create a scatter plot or a run sequence plot to double-check for sinusoidal patterns. You could also make a lag plot; an elliptical pattern would confirm that the data is sinusoidal.
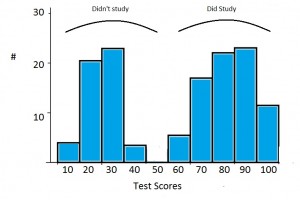
Sometimes, what appears to be a bimodal distribution is actually two unimodal (one-peaked) distributions graphed on the same axis. For example, this image shows a bimodal distribution for a group of students who did not study (the left peak) and a group of students who did study (on the right). 
A mixture of two normal distributions will not be bimodal unless there is a large difference between their means — typically bigger than the sum of the individual distribution’s standard deviations [6].
Unimodal Distributions.
In comparison, unimodal distributions have a single peak, or mode. 
Several unimodal distributions shown on the same graph. [7]
Multimodal Distributions
Multimidal distributions have more than two peaks. If you can’t clearly find one peak or two peaks in a graph, the likelihood is that you either have a uniform distribution (where all the peaks are the same height) or a multimodal distribution, where there are several peaks of the same height.
Tip: Although you might commonly associate “mode” with being the most frequently occurring number in a data set, the term mode actually has two meanings in statistics, which can be confusing: it can either be a local maximum in a chart, or it can be the most frequently occurring score in a chart. The “mode” in bimodal distribution means a local maximum in a chart (i.e. a local mode). The two terms actually mean the same thing, as the most commonly found item in a data set will have a peak. But when you’re trying to categorize graphs, it’s easier to think of the mode as a “peak” rather than a common number. This helps especially if the axes are not labeled.
Fun fact: While the bell curve is normally associated with grades (i.e. 5% of the class will get an A and 10% of the class will get a B), it’s also quite normal to have a bimodal distribution where roughly half of a class will do very well (getting As and Bs) and the other half of the class will receive poor grades (Ds and Fs). Bimodal distributions are very common in college freshman mathematics classes!
References
- Image credit: Maksim|Wikimedia Commons. CC 4.0.
- Measures of spread; shape
- Particle Size Distribution Functions:
- Lee, C. et al. (2015) Rapid intensification and the bimodal distribution of tropical cyclone intensity. Nature Communications. DOI: 10.1038/ncomms10625
- Kim, S. et al. Decision-Tree-Based Classification of Lifetime Maximum Intensity of Tropical Cyclones in the Tropical Western North Pacific
- Schilling, M. et al. (2002). Is Human Height Bimodal? The American Statistician, Vol. 56, No. 3, (Aug., 2002), pp. 223-229
- Image credit: Grendelkhan|Wikimedia commons. CC 4.0.
- An Attention-Sensitive Memory Trace in Macaque MT Following Saccadic Eye Movements. PLOS Journal. https://journals.plos.org/plosbiology/article/figure?id=10.1371/journal.pbio.1002390.g004