Probability Distributions > Compound Probability Distribution
What is a Compound Probability Distribution?
A compound probability distribution has random variables drawn from a “compound” parametric distribution, where one or more of the distributions parameters (i.e. the mean) are taken from other probability distributions.
Compound Random Variables
Simply put, compound random variables are any variables drawn from a compound distribution. They are defined more precisely with the following equation:
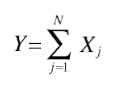
Where:
- Y is a compound random variable,
- Xj is a group of iid random variables from a single experiment,
- N is a non-negative, discrete random variable.
Example
Princeton University professor Sam Wang created a compound probability distribution for the probability of Democrats or independent getting control of the senate in 2014. The distribution was an amalgam of all contested races in that year.
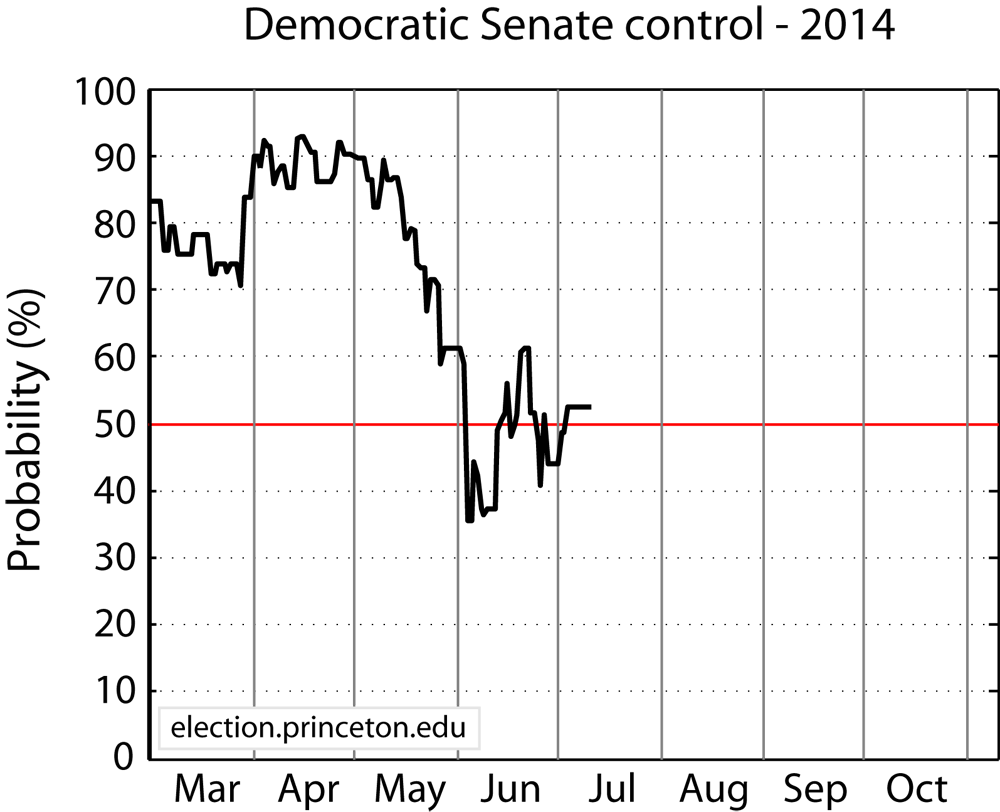
As you can tell, the compound graph is much easier to read than one where all the individual races are listed: You’re able to see the overall trend, instead of trying to make sense of a large number of individual graphs.
Mixture vs. Compound Distribution
A mixture distribution is a blend of a countable, finite number of distributions (in rare cases, you could have a countably infinite* number of distributions). The compound distribution is the general case of a mixture distribution, where the component distributions are uncountable.
* The term “countably infinite” comes from set theory, and means that the set has elements that are in a one-to-one correspondence with the set of natural numbers. Although it would take forever to count all of the elements in the set, you could theoretically get to a certain element in a finite period of time.
References
Cassady, R. & Nachlas, J. (2008). Probability Models in Operations Research. CRC Press.
Fox, G. et al., (2015). Ecological Statistics: Contemporary Theory and Application. Oxford University Press.