What is a Pólya Distribution?
The Pólya distribution has applications in fields as diverse as genetics, insurance, and modeling epidemics.
The multivariate Pólya distribution, sometimes called the Dirichlet-multinomial distribution or Dirichlet compound multinomial distribution, is an extension of the univariate beta binomial distribution.
Process and PMF for the Pólya Distribution
The distribution models a simple process: draw a random ball from an urn containing r red balls and N − r black balls. Record the color of the ball, then return the ball to the urn with c additional balls of the same color. Repeat the process for n draws. If X is the number of red balls removed in the first n trials, then the random variable X follows a Pólya distribution.
The probability mass function is [3]:
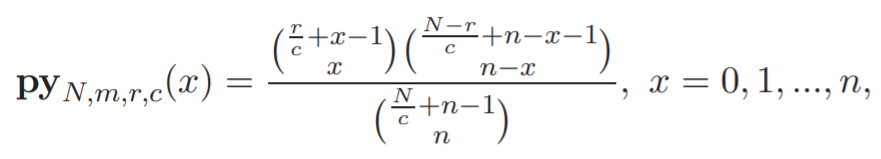
Where N, n, r, and c are natural numbers.
When the sample size is large enough, the Pólya distribution can be estimated with the binomial distribution.
References
[1] Kaiser, H. & Stefansky, W. A Polya Distribution for Teaching. The Teacher’s Corner. Retrieved November 13, 2021 from: https://www.jstor.org/stable/2682866
[2] Marshall, A. (1990). Bivariate Distributions Generated from Pólya-Eggenberger Urn Models. Journal of Multivariate Analysis 35, 48-65.
[3]Teerapabolarn, K. (2014). An Improved Binomial Distribution to Approximate the Pólya Distribution. International Journal of Pure and Applied Mathematics
Volume 93 No. 5, 629-632