Probability Distributions > Heavy Tailed Distribution / Light Tailed Distribution
What is a Heavy Tailed Distribution?
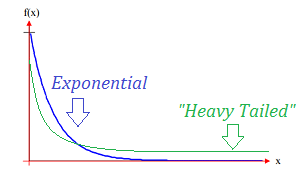
A heavy tailed distribution has a tail that’s heavier than an exponential distribution (Bryson, 1974). In other words, a distribution that is heavy tailed goes to zero slower than one with exponential tails; there will be more bulk under the curve of the PDF. Heavy tailed distributions tend to have many outliers with very high values. The heavier the tail, the larger the probability that you’ll get one or more disproportionate values in a sample.
Characteristics of the Heavy Tailed Distribution
If you take a random sample from the distribution, you’re likely to end up with a sample made up from mostly small values. But there will probably be one or more very large values that will throw your statistics off. For example, if you sample from the income of people in the United States, the bulk of your data will be relatively small—around $50,000. However, one or two values in your sample could be ridiculously large (i.e. outliers). You could draw 99 items that are around $50,000, then a “Bill Gates”—he earns several billion dollars per year.
These large values tend to skew your sample statistics: the mean would be very misleading (for the above example, it would be in the millions of dollars), the sample variance will probably be very large and the sample mean usually underestimates the population mean. Another couple of quirks with heavy tails:
- The Central Limit Theorem doesn’t work.
- Some moments don’t exist, so order statistics are used instead.
Heavy Tailed Distributions in the Real World
Many real world situations are heavy tailed, including:
- The top 0.1% of the population in the USA owns as much as the bottom 90% (Guardian).
- File sizes in computers tend to be small, with a few very large files thrown into the mix (Columbia).
- Web page sizes and computer systems’ workloads tend to be heavy-tailed (Stanford).
- Insurance Payouts and Financial Returns follow a similar pattern (Wolfram).
Heavy Tailed Distribution Examples
Many distributions are heavy tailed, including:
- Cauchy Distribution
- Fréchet Distribution
- LogNormal Distribution
- Pareto Distribution
- Student’s t Distribution
- Zipf Distribution
Cauchy distribution.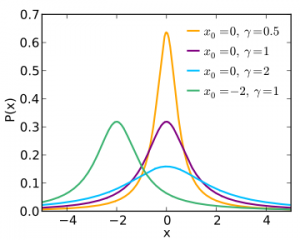
The Cauchy is similar to a normal distribution, except it has heavier tails and a taller peak. It is widely known for the fact that it’s expected value does not exist.
Log normal distribution.
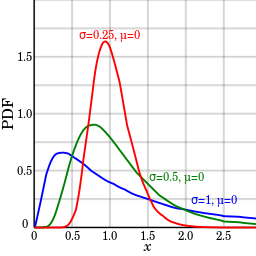
A lognormal (log-normal or Galton) distribution is a probability distribution with a normally distributed logarithm.
Heavy Tailed Subclasses
Fat tail distribution: A heavy tailed distribution with infinite variance. Note that some authors use the term “fat tail” and “heavy tail” interchangeably, especially in finance and trading.
Regularly varying: the tails’ behavior deviates from pure power laws (Mikosch, 1999).
Subexponential: A distribution where the largest value in a sample makes a very large contribution to the overall sum (Mikosch, 1999).
Long-tailed distribution: A heavy-tailed distribution with a long tail. Some authors use the term long-tail as a synonym for “light-tailed” (see definition below), although the general consensus is that a long-tail is a subset of heavy-tail. To add to the confusion, others make a distinction between a thin tail (as compared to the exponential) and a tail with a long appearance— as in a very, very, very long tail (imagine 50 standard deviations from the mean, and you’ll begin to get the distinction). The key here is to read the author’s intention very carefully is they are using the term “long tail”.
What is a Light Tailed Distribution?
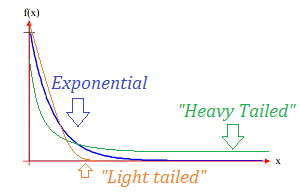
Probability distributions that have thinner tails than an exponential distribution are light-tailed distributions. They go to zero much faster than the exponential, and so have less mass in the tail. The Gumbel distribution is an example of a light-tailed distribution. Most distributions that you’re introduced to in elementary statistics (e.g. the normal distribution & t-distribution) are actually light-tailed; These don’t reflect “real world” data very well Nair et. al, 2013).
References
Bryson, M. (1974). Heavy Tailed Distributions: Properties and Tests. Technometrics 16(1):61-68 (February 1974).
Mikosch, T. (1999). Regular Variation, Subexponentiality, and Their Applications in Probability Theory.
Retrieved December 10, 2017 from: https://www.eurandom.tue.nl/reports/1999/013-report.pdf
Nair, J. et al., (2013). The fundamentals of heavy tails (PPT). Retrieved December 7, 2017 from: http://users.cms.caltech.edu/~adamw/papers/2013-SIGMETRICS-heavytails.pdf