What is a Rademacher Distribution?
The Rademacher distribution is a recoding of the Bernoulli distribution with two possible values {-1, 1}. It’s second moment (the variance) equals 1; all other moments equal 0 [1]. It is named after German-American mathematician Hans Rademacher and denoted Rad½.
Like the Bernoulli, a random variable has a 50% chance of a success and 50% chance of failure.
- Bernoulli: 0 (failure) and 1 (success),
- Rademacher: -1 (failure) and 1 (success).
The distribution is used for formulating statistical proofs, random sampling [1], and bootstrapping , where weights dg = {−1, 1} are called Rademacher weights [2].
PMF of the Rademacher Distribution
The Rademacher distribution is a discrete probability distribution and so can be described by a probability mass function:
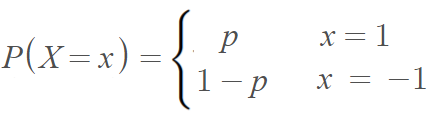
The distribution can also be written in terms of the Dirac Delta function:
f(k) = ½ (δ(k – 1) + δ(k + 1).
Rademacher Random Variables
Rademacher random variables can be defined in terms of Bernoulli random variables. If Y is a Bernoulli random variable, then X = 2Y −1 is a Rademacher random variable [3]. Conversely, if X is a Rademacher random variable, then (X + 1) /2 is a Bernoulli random variable.
These variables can also be defined in terms of the Laplace distribution. Given a Rademacher random variable X, if Y ~ Exp(λ) is independent from X, then XY ~ Laplace (0, 1/λ).
A sequence of successive sums of Rademacher random variables is a random walk.
References
[1] Contreras, D. (2021). Estimation of Flexibility Potentials in Active Distribution Networks. Books on Demand.
[2] Miller, D. & Cameron, C. A Practitioner’s Guide to Cluster-Robust Inference.
[3] Border, C. Supplement 2: Review Your Distributions. Retrieved January 1, 2022 from: http://www.math.caltech.edu/~2016-17/2term/ma003/Notes/DistributionReview.pdf.