The Kumaraswamy distribution is a two-variable family of distributions that is bounded at one and zero. It is flexible and can be used to model a variety of shapes, and its probability density function and cumulative distribution function can be written in very simple terms.
Comparison of the Kumaraswamy distribution the Beta Distribution
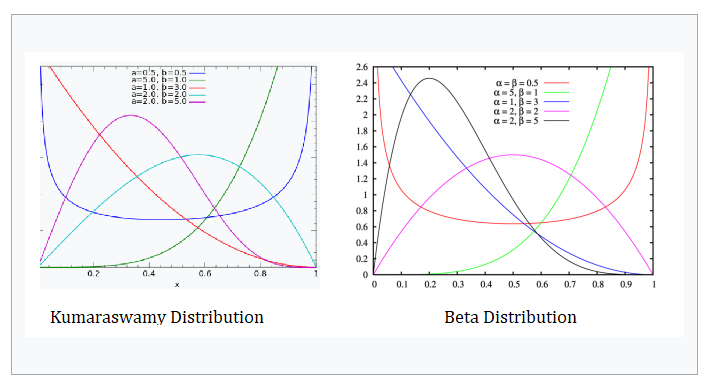
The Kumaraswamy distribution is very similar to the beta distribution and has the same basic shape. So similar in fact, it’s often referred to as a “Beta-like” distribution. However, the Kumaraswamy distribution is simpler to use and in some situations more tractable. It is often preferred over the Beta in part because the CDF has the closed form:
P(x) = 1 – (1 – xa)b).
Unlike the beta, the Kumaraswamy distribution’s CDF doesn’t contain the incomplete Beta function, which makes it much easier to work with (Michalowicz et al., 2013). The PDF and quantile functions also have a closed form, making the Kumaraswamy distribution a more practical choice for many applications—especially simulation studies. Other notable advantages over the beta include explicit formula for moments of order statistics and a simple formula for generation of random variables (Ishaq et al., 2019).
PDF for the Kumaraswamy distribution
The probability distribution function for the Kumaraswamy distribution is:
![]()
In this equation a and b are non-negative shape parameters.
References
Ishaq et al., (2019). On some properties of Generalized Transmuted Kumaraswamy distribution. Pakistan Journal of Statistics and Operation Research; Lahore Vol. 15, Iss. 3, (2019): 577-586.
Michalowicz, J. et al., (2013). Handbook of Differential Entropy. CRC Press.