Probability Distributions > Erlang Distribution
What is the Erlang Distribution?
The Erlang distribution (sometimes called the Erlang-k distribution) was developed by A.K. Erlang to find the number of phone calls which can be made simultaneously to switching station operators. Erlang was a telecommunications engineer for the Copehagen Telephone Company; his formulas for loss and waiting time were used by many telephone companies, including the British Post Office. Erlang’s distribution has since been expanded for use in queuing theory, the mathematical study of waiting in lines. It is also used in stochastic processes and in mathematical biology.
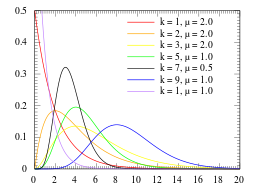
The Erlang distribution is a specific case of the Gamma distribution. It is defined by two parameters, k and μ, where:
- k is the shape parameter. This must be a positive integer (an integer is a whole number without a fractional part). In the Gamma distribution, k can be any real number, including fractions.
- μ is the scale parameter. Must be a positive real number (a real number is any number found on the number line, including fractions).
The probability density function of the Erlang distribution is:
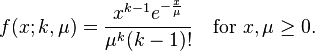
The factorial(!) in the denominator is the reason why the distribution is only defined for positive numbers. An equivalent form of the density function for this distribution includes λ, a measure of rate, which is related to μ in the following way:
μ = 1/λ.
where λ represents the number of items or calls expected in a given amount of time.
Statistics of the Erlang Distribution
Relationship to Other Distributions
- The Gamma distribution is a generalized form of the Erlang distribution.
- If the shape parameter k is 1, the distribution is the same as the exponential distribution.
- If the scale parameter is 2, the distribution is the same as a chi-squared distribution with 2 degrees of freedom.