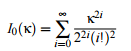Probability Distributions > Von Mises Distribution
What is the Von Mises Distribution?
The Von Mises distribution, also known as the circular normal or Tikhonov distribution, is a captivating continuous probability distribution that spans a range from 0 to 2π. This intriguing distribution is akin to the normal distribution, but with a unique twist – its coordinates exist on a circular plane. Thus, envisioning the Von Mises distribution as a specialized variant of the Von Mises-Fisher distribution, which extends to multi-dimensional spheres, might help in grasping its essence.
Initially described by the brilliant mind of Richard von Mises in 1918, this distribution sought to model the fascinating world of atomic weights. Today, its applications have broadened, and it can be found modeling a diverse array of phenomena.
- Brownian motion (Physics),
- Epidemiology (spread of disease),
- Interference Alignment (Signal Processing),
- Privacy-preserving algorithms in (Machine Learning).
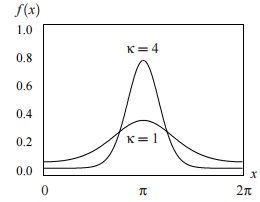
The general form of the Von Mises PDF is:
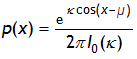
Where:
- μ = mean direction of the distribution.
- κ = a shape parameter.
- I00(κ) = modified Bessel function with order zero. Defined for all κ as:

X ~ von Mises (κ, μ) or X ~ CN(κ, μ) indicates random variable X has a von Mises distribution with shape parameter κ and location parameter μ.
CDF
The cumulative distribution function for this distribution is:
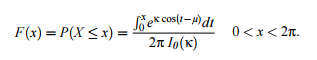
Other Characteristics
The median and mean of X = zero.
The following are intractable:
- Characteristic function,
- Hazard function,
- Inverse distribution function,
- Kurtosis,
- Population variance,
- Skewness.
Software
- Dataplot (open-source) VONPPF command.
- Oriana for Windows.
- Circstats for R (open-source).
- Circstat for MatLab.
References
Grafarend, E. & Awange. J. (2012) Applications of Linear and Nonlinear Models: Fixed Effects, Random Effects. Springer Science & Business Media, Aug 15.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Von Mises, R. (1981): Uber die Ganzzahligkeit der Atomgewichte und verwandte Gragen. Phys. Z. 19 (1918), 490-500.