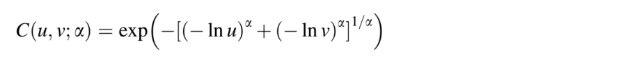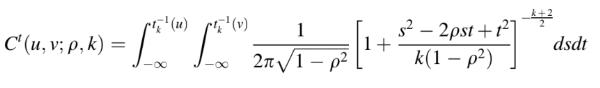Probability Distribution: List of Statistical Distributions >
Copula distributions contain copulas (from the Latin link)—the joint distributions of random variables. They enable us to identify dependencies in multivariate distributions; Any multivariate distribution can be modeled with a separately specified set of marginal distributions and the copula.
Each random variable U1, U2, …, Up has a marginal uniform distribution U(0, 1).
Copulas and Copula distributions are used in many areas of statistics and finance. For example, copulas play a key role in pricing securities (Haugh, 2016). In risk analysis, model selection for Copula distributions can be used to link multiple risk processes (Cruz et al., 2015).
In linguistics, grammatical copulas link parts of a sentence. Although they share the same name, they are mathematically unrelated.
Types of Copula Distributions
The family of Copula Distributions include a wide variety of functions with differing tail behavior. Four of the most common Copula functions, along with their respective Probability Density Functions are (Xue et al, 2019):
- Binary Clayton Copula Distribution function: This variant has an asymmetrical tail with an upper tail correlation coefficient of zero. It is suitable for finding the lower tail correlation between variables:
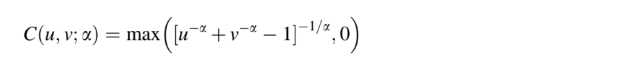
- Binary Frank Copula distribution function: This type has a symmetrical, independent tail with correlation coefficients of zero for both tails:
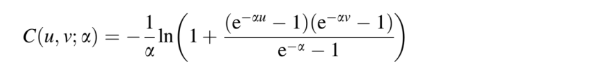
- Binary Gumbel Copula Distribution function: This type has an asymmetrical tail with a lower tail correlation coefficient of zero. It is suitable for calculating upper tail correlation between variables:

- Binary t-student Copula Distribution function: This variant has a thick symmetrical tail, so sensitive to changes in random variables affecting tails.

References
Cruz, M. et al. (2015). Fundamental Aspects of Operational Risk and Insurance Analytics: A Handbook of Operational Risk (Wiley Handbooks in Financial Engineering and Econometrics) 1st Edition. Wiley.
Gupta, A. 2013. Risk Management and Simulation 1st Edition. CRC Press.
Haugh, M. (2016). An Introduction to Copulas. Retrieved April 13, 2019 from: An http://www.columbia.edu/~mh2078/QRM/Copulas.pdf
Xue et al. (2019). Proceedings of PURPLE MOUNTAIN FORUM 2019-International Forum on Smart Grid Protection and Control, Volume 2. Springer.