Contents:
- Bivariate Normal
- Multivariate Normal
1. What is a Bivariate Normal Distribution?
The bivariate normal distribution is a fascinating combination of two independent random variables that are both normally distributed. This creates an elegant, three-dimensional bell curve when visualized – representing the interplay between these two distinct elements. Exploring this concept allows for deeper insight into how multiple variables can interact and create novel outcomes.
Francis Galton was a trailblazer in mathematics, pioneering the exploration of bivariate normal distributions and discovering intriguing patterns between parents’ heights and those of their children. This captivating field also had other early nineteenth century luminaries, such as Bravais, Gauss, Laplace and Plana all making significant contributions to its development.
With the bivariate distribution, there’s no single way to define and describe it. But one thing always remains true: its characterization is a topic of much debate! From common perspectives like joint probability distributions or correlation coefficients – this concept continues to fascinate scholars across many disciplines.
- Random variables X & Y are bivariate normal if aX + bY has a normal distribution for all a,b∈R.
- X and Y are jointly normal if they can be expressed as X = aU + bV, and Y = cU + dV (Bertsekas & Tsitsiklis, 2002)
- If a and b are non-zero constants, aX + bY has a normal distribution (Johnson & Kotz, 1972).
- If X – aY and Y are independent and if Y – bx and X are independent for all a,b (such that ab ≠ 0 or 1), then (X,Y) has a normal distribution (Rao, 1975).
PDF of the Bivariate Normal Distribution.
The bivariate normal distribution can be defined as the probability density function (PDF) of two variables X and Y that are linear functions of the same independent normal random variables (adapted from Wolfram):
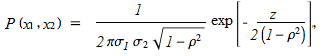
Where:
- μ = mean
- &sigma = standard deviation
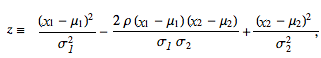
- And:

- ρ correlation of x1 and x2.
- V x12= covariance of x1 and x2.
If p = 2, this is equal to the bivariate normal distribution.
For some excellent gifs that show what happens when a few of these parameters are changed, check out Brad Hartlaub’s page at Kenyon college. This one shows what happens when μ1 is changed:
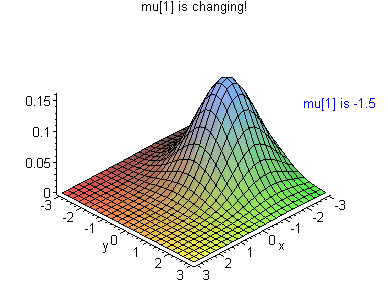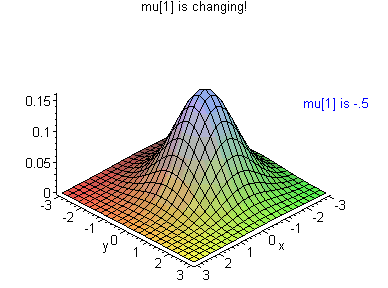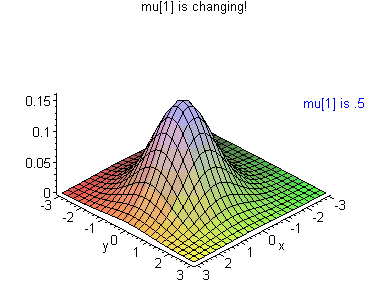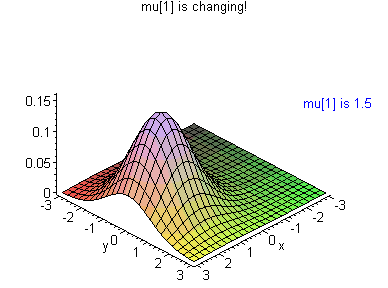
2. What is a Multivariate Normal Distribution?
With the bivariate normal distribution, two random variables can be easily visualized — but when more than two are involved, it’s a different story. The multinormal is hard to make sense of without matrix algebra proficiency or some other form of technical savviness – however it still stands as one of the most crucial distributions in understanding today’s multi-dimensional statistics.
The multivariate normal distribution is most often described by its joint density function. A multivariate normal p x 1 random vector X, with population mean vector μ and population variance-covariance matrix σ, will have the following joint density function:
![]()
Where:
- |Σ| = determinant of the variance-covariance matrix Σ
- Σ-1 = inverse of the variance-covariance matrix Σ
References:
Balakrishnan,N. & Lai, C. (2009) Continuous Bivariate Distributions.
Johnson & Kotz. (1972) Distributions in Statistics: Continuous Multivariate Distributions.
Bertsekas & Tsitsiklis (2002). Introduction to Probability (1st ed.).
Rao, C. (1975). Some Problems in the Characterization of the Multivariate Normal Distribution.
Wolfram Mathworld. BND. Retrieved August 4, 2017 from: http://mathworld.wolfram.com/BivariateNormalDistribution.html