Probability and Statistics > Non normal Distributions > Gamma Distribution
The gamma distribution is a family of right-skewed, continuous probability distributions. These distributions are useful in real-life where something has a natural minimum of 0. For example, it is commonly used in finance, for elapsed times, or during Poisson processes.
Gamma Distribution PDF
If X is a continuous random variable then the probability distribution function is:
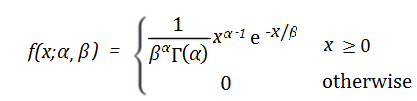
Where
- Γ(x) = the gamma function,
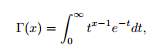 .
. - α = The shape parameter.
- β (sometimes θ is used instead) = The rate parameter (the reciprocal of the scale parameter).
α and β are both greater than 1.
When α = 1, this becomes the exponential distribution.
When β = 1 this becomes the standard gamma distribution.
Alpha and beta define the shape of the graph. Although they both have an effect on the shape, a change in β will show a sharp change, as shown by the pink and blue lines in this graph:
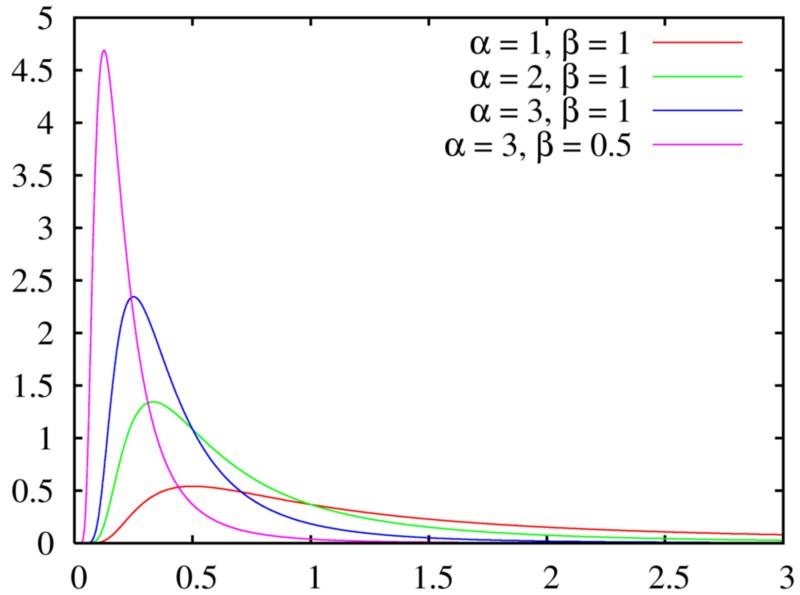
You can think of α as the number of events you are waiting for (although α can be any positive number — not just integers), and β as the mean waiting time until the first event. If α (number of events) remains unchanged but β (mean time between events) increases, it makes sense that the graph shifts to the right as waiting times will lengthen. Similarly, if the mean waiting time (β) stays the same but the number of events (α) increases, the graph will also shift to the right. As α approaches infinity, the gamma closely matches the normal distribution.
Mean, Variance, MGF
Mean: E(X) = αβ
Variance: var(X) = αβ2
Moment generating function: MX (t) = 1 /(1 − βt)α
(Artemiou, 2009)
How to Find Gamma Distribution Probabilities in Excel
Step 1: Type “=GAMMA.DIST(” into an empty cell.
Step 2: Type the value where you want to find the probability. For example, if you want to find the probability at x=6, the function becomes “=GAMMA.DIST( 6”
Step 3: Type your α and β values, separated by a comma. For example, if your α is 3 and β is 2, the function becomes: “=GAMMA.DIST( 6, 3, 2”
Step 4: Type FALSE, close the parentheses and then hit the “enter” key. The entire function is “=GAMMA.DIST( 6, 3, 2, FALSE” Excel will return the probability as 0.112020904.
Tip: To find the cumulative probability, type TRUE instead of FALSE in Step 4.
MATLAB.
The gamma distribution is calculated in MATLAB using the prob.GammaDistribution object. You can find full instructions on how to find the distribution in MATLAB here on the MathWorks site.
Related Distributions
The gamma is a special case of the Tweedie distribution (when p = 2).
For integer degrees of freedom, the Wishart distribution is the multivariate counterpart of the gamma distribution.
The inverse gamma distribution has the same distribution as the reciprocal of a gamma distribution. It is mainly used in Bayesian hypothesis testing.
The Erlang distribution and chi-square distribution are special cases of the gamma distribution. The Erlang distribution happens when α is any positive integer. The exponential distribution is also a special case of the gamma distribution. The gamma and exponential are very similar, as shown by this graph. The two curves have identical means but different standard deviations:
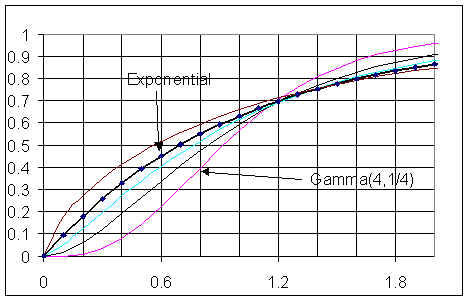
The Inverse Gaussian also has a similar shape to the gamma. In fact, they can look exactly the same given the right parameters. However, it’s easier to produce extremely large values with the inverse Gaussian.
References
Artemiou, A. (2009). Chapter 4 — Lecture 4 The Gamma Distribution and its Relatives. Retrieved November 3, 2017 from: http://www.math.mtu.edu/~aartemio/Courses/Stat318/Lectures/Chapter4/Chapter4_Lecture4.pdf.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 534, 1987.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 103-104, 1984.