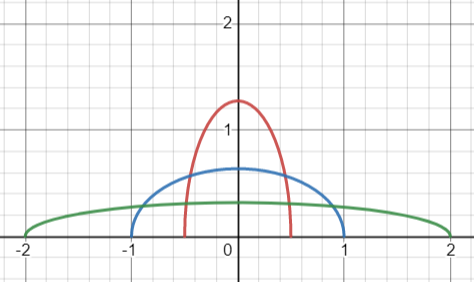
The intriguing semicircle distribution, also known as Wigner’s semicircle distribution, is a continuous probability phenomenon whose shape could be likened to the classic half-moon. Centered around origin (0, 0), this captivating mathematical gem stretches outwards in either direction with an adjustable radius of R > 0 over the interval [-R , R].
The probability density function of the semicircle distribution is:
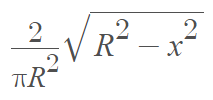
A variant is the power semicircle distribution PS(θ, R), which has PDF:
fθ(x, R) = c′θ, R(f0(x; R))2θ + 1) = cθ, R (R2 – x2)θ + ½ 1|x| ≤ , R
Where R is the range parameter and θ is the shape parameter.
Uses of the Semicircle Distribution
The semicircle distribution is a staple of many mathematical topics, from applied mathematics to physics. E.P Wigner demonstrated it as an important element in random matrices and the local semicircle law states its eigenvalue lies close by this distribution [1]. It also features in quantum Brownian motion on Fock space [2], Markov chains with Young diagrams[3] and even the free version of central limit theorem [4]. Clearly, there’s much more complexity here than meets the eye!
References
Graph of Wigner’s semicircle distribution created with Desmos.
[1] Benaych-Georges, F. & Knowles, A. Lectures on the local semicircle law for Wigner matrices.
[2] Hashimoto, Y. DEFORMATIONS OF ITHE SEMICIRCLE LAW DERIVED FROM RANDOM WALKS ON FREE GROUPS.
[3] Arizmendi, O. & Perez-Abreu, V. (2010). ON THE NON-CLASSICAL INFINITE DIVISIBILITY OF POWER SEMICIRCLE DISTRIBUTIONS. Communications on Stochastic Analysis. Vol. 4, No. 2. 161-178. Retrieved December 30, 2021 from: http://personal.cimat.mx:8181/~pabreu/4-2-02%5B221%5D.pdf
[4] Barndorff-Nielsen, O. & Thorbjørnsen, S. Levy laws in free probability.