The array distribution refers to the conditional distribution of independent random variables X1 (given X2, … , Xn). As such, it is often used as a synonym for a conditional distribution (for example, Kotz et al. [1], Giri & Banerjee [2], Wadworth & Bryan [3]).
The Encyclopedia of Statistical Sciences [4] gives an example of an array distribution of X
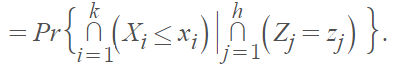
The variance of this distribution is called the array variance; if the variance doesn’t depend on X2, … ,Xn , the variation is homoscedastic [5]. Its variance-covariance matrix is called the array-variance-covariance matrix.
Array Distribution in Applied and Theoretical Statistics
As pointed out above, the array distribution is commonly used as a synonym for conditional distribution. They do mean the same thing, but you’re more likely to see the term array distribution in applied statistics and conditional distribution in theoretical statistics [6]. The array distribution is denoted by
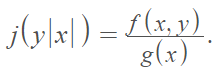
You can think of this as the density of y for a fixed value of x.
References
[1] Kotz, S. et al. (2000). Continuous Multivariate Distributions, Volume 1 Models and Applications. John Wiley & Sons.
[2] Giri, P. & Banerjee, J. (2021). Statistical Tools and Techniques. Academic Publishers.
[3] Wadsworth, G. & Bryan, J. (1960). Introduction to Probability and Random Variables. McGraw-Hill.
[4] Vidakovic , B. et al. (Eds.) (2005). Encyclopedia of Statistical Sciences, Volume 3. Wiley.
[5] Johnson, Kotz, and Balakrishnan, (1994), Continuous Univariate Distributions, Volumes I and II, 2nd. Ed., John Wiley and Sons.
[6] Haight (ed.) (1963). Mathematical Theories of Traffic Flow. Elsevier Science