Probability Distributions > Inverse Gaussian Distribution
What is the Inverse Gaussian Distribution?
The Inverse Gaussian Distribution, also called the Wald or normal-inverse Gaussian, is an exponential distribution with a single mode and long tail. The distribution is used to model non-negative, positively skewed data and has a wide variety of applications in business, survival analysis, finance, medicine, and even in labor dispute resolution. The distribution’s tail decreases slowly compared to the normal distribution. Therefore, it’s suitable for modeling phenomena where there is a greater likelihood of getting extremely large values compared to the normal distribution.
The “inverse” in the name is misleading; it doesn’t actually refer to the inverse of a distribution. Originally developed for the theory of Brownian motion (the random movements of particles in liquid), it got the name Inverse Gaussian in 1956, when Tweedie noted that there is an inverse relationship between distance covered in unit time and time to cover a unit distance.
Probability Density Function
The probability density function for the distribution is:
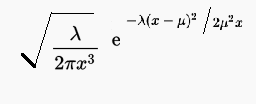
Where:
- μ a location parameter (the mean) and
- λ a scale parameter.
Both parameters must be positive numbers.
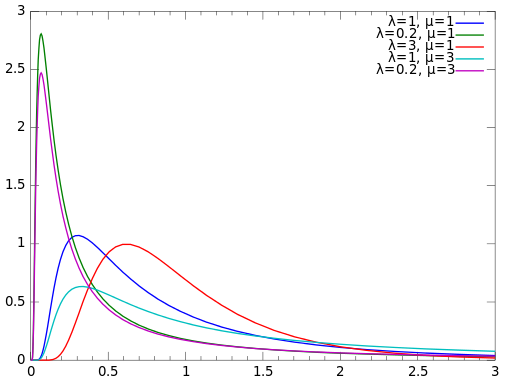
Similarities to Other Distributions
Although the inverse Gaussian distribution is sometimes called the “normal inverse” distribution, it is not to be confused with the inverse normal distribution, which is a way to find probabilities for a normal distribution.
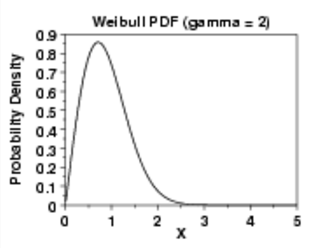
This distribution has a similar shape to the Weibull distribution, but has the advantage it’s easier to estimate probabilities (the Weibull, with three parameters, is more difficult).
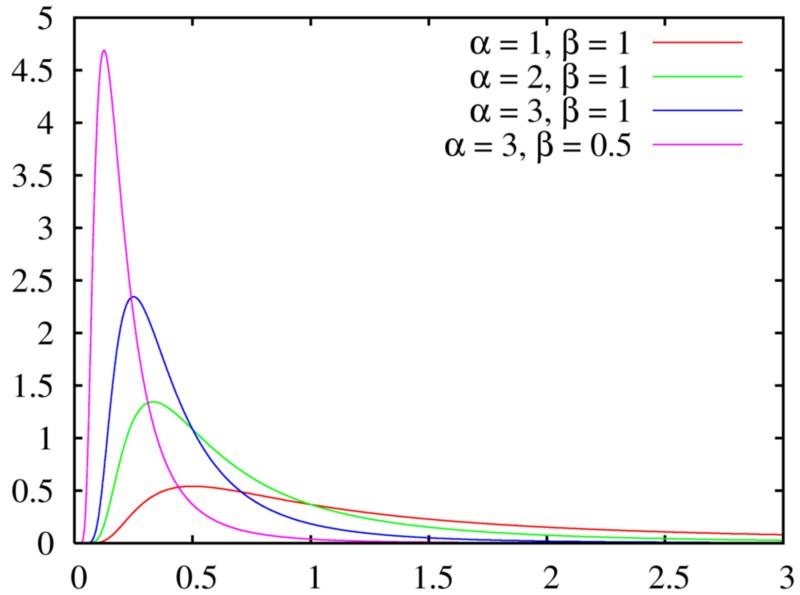
The Gamma distribution also has a similar shape. In fact, they can look exactly the same given the right parameters. However, it’s easier to produce extremely large values with the inverse Gaussian.
References:
Schrodinger E., 1915, Zur Theorie der Fall-und Steigversuche an Teilchen mit Brownscher Bewegung, Physikalische Zeitschrift 16, 289–295.
Tweedie, M. C. K. (1956). Some Statistical Properties of Inverse Gaussian Distributions. Virginia Journal of Science, 7, 160-165.