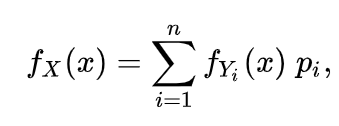The hyperexponential distribution (also called a mixed exponential or parallel m-phase exponential distribution) is created by a probabilistic mixture of exponential distributions. It is a generalization of the Erlang distribution and a special case of the phase-type distribution (made by a convolution or mixture of exponential distributions) [1].
It’s called hyperexponential because the distribution always has a coefficient of variation greater than 1 [2].
Hyperexponential Distribution Parameters and Shape
The hyperexponential distribution is defined over the half-open interval [0, ∞). The shape of the distribution is determined by two vectors α (phase probabilities with values from 0 to 1) and λ (phase rates, which are real-valued).
- Yi = an exponentially distributed random variable with rate parameter i.
- pi = probability that X will have an exponential distribution with rate λ.
Generally speaking, the hyperexponential distribution is monotonically decreasing with light tails. This means that the PDF decreases exponentially for large x-values.
Stages of a Hyperexponential Distribution
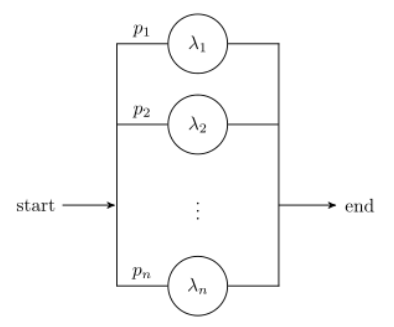
The hyperexponential distribution arises when a process has alternate phases, meaning that only one of the many possible parallel phases will occur in any particular experiment. If the alternate phases have independent exponential distributions, then the distribution is hyperexponential [3].
Hyperexponential distributions can have any number of stages. For each stage, parameters must be specified defining the probability of receiving service and rate of service at each stage.
For example, a two-stage hyperexponential, created from two exponentials, has three parameters: p, λ1 and λ2 [4]:
- p: the probability of receiving service at rate λ1.
- p – 1: the probability of receiving service at rate λ2.
References
Queueing System Image: Gareth Jones, CC BY-SA 3.0
[1] Package ‘sdprisk’.
[2] (2013) Hyperexponential Distribution. In: Gass S.I., Fu M.C. (eds) Encyclopedia of Operations Research and Management Science. Springer, Boston, MA.
[3] Iyer, R. (1999). Important Distributions. Retrieved April 2, 2021 from: https://www.statisticshowto.com/erlang-distribution/
[4] CS 547 Lecture 14: Other Service Time Distributions