Probability Distributions > Beta-Binomial & Beta-Bernoulli Distribution
A beta-binomial distribution is a mixture of a binomial and beta distribution, so you may find it helpful to read these articles first:
What is the Beta-Binomial Distribution?
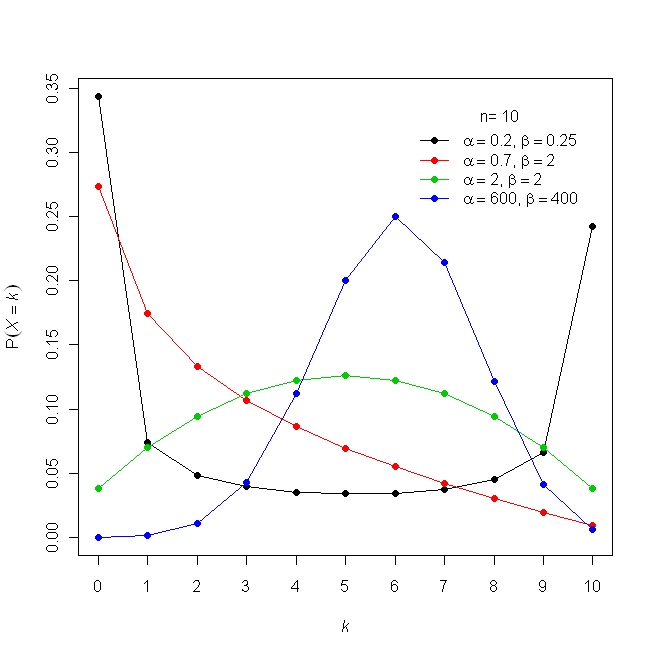
The beta-binomial distribution is one of the simplest Bayesian models. It is widely used, including in epidemiology, intelligence testing and marketing.
A distribution is beta-binomial if p, the probability of success, in a binomial distribution has a beta distribution with shape parameters α > 0 and β > 0. The shape parameters define the probability of success.
- For large values of α and β the distribution approaches a binomial distribution.
- When α and β both equal 1, the distribution equals a discrete uniform distribution from 0 to n.
- When n = 1, the distribution is the same as a Bernoulli distribution.
One major difference between a binomial and beta-binomial is that in a binomial distribution, p is fixed for a set number of trials; in a beta-binomial, p is not fixed and changes from trial to trial.
Deriving the Formula
Let’s say you have m items on an test, and each item is tested n times. The binomial distribution formula is:
P(X=xi) = nCxi * Pxii * (1 – pi)n – xi, i =1,2,3,…,n
Where:
- P = binomial probability,
- xi = total number of “successes” (pass or fail, heads or tails etc.) for the ith trial,
- pi = probability of a success on an individual trial,
- n = number of trials,
Perhaps the simplest way to think of the beta-binomial is to take the above formula and think of p as being randomly drawn from a beta distribution.
However, to write the formula out in full, take the probability density function for the Beta Distribution:
![]()
…and combine it with the binomial distribution formula to get a joint pdf.
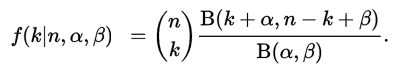
Which can also be written (using Beta distribution properties) as: