What are Multivariate Gamma Distributions?
The Multivariate Gamma Distributions are generalizations of the univariate gamma distributions. Generally speaking, a random vector has a multivariate gamma distribution if it has gamma marginals [1].
There are dozens of different extensions of multivariate gamma distributions; some are defined by density functions, while others are defined by other formulas. However, the generalized multivariate gamma distribution probability density function can be defined as [2]:
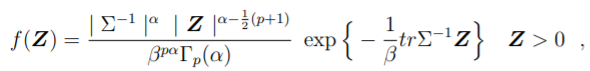
Where Γpα is the multivariate gamma function.
Types of Multivariate Gamma Distributions
Many different types are found in the literature, including:
- Dussauchoy and Berland’s [3] defined by a characteristic function,
- Gaver’s multivariate gamma distribution [4], which generates a multivariate distribution with a mixture of gamma variables with negative binomial weights.
- Krishnamoorthy and Parthasarathy’s [5] p-variate gamma distribution (also called the Wishart-chi-square distribution) exists for all positive integer degrees of freedom v and at least for all real values v > p-2, p ≥ 2.
References
[1] Viraswami, K. (1991). On Multivariate Gamma Distributions. Retrieved January 1, 2022 from: https://escholarship.mcgill.ca/downloads/76537233r?locale=en
[2] Das, S. & Dey, D. On Bayesian Inference for Generalized Multivariate Gamma Distribution. Retrieved January 1, 2022 from: http://www2.stat.duke.edu/~sd83/Research/das-dey-mult-gamma.pdf
[3] Dussauchoy, A. & Berland, R. (1974). A multivariate gamma type distribution whose marginal laws are gamma, and which has a property similar to a characteristic property of the normal case. Statistical Distributions in Scientific Work, Vol. 1. Patil, G. et al (eds.). D. Reidel, Boston. 319-328.
[4] Gaver, D. P. (1970). Multivariate gamma distributions generated by mixture. Sankyhya Series A, 32, 123-126.
[5] Krishnamoorthy, A. S. and Parthasarathy, M., A multivariate gamma type distribution, Ann. Math. Stat. 22
(1951), 549-557.