A bivariate distribution (or bivariate probability distribution) is a joint distribution with two variables of interest. The bivariate distribution gives probabilities for simultaneous outcomes of the two random variables.
- A discrete joint distribution has at most a countable number of possible outcomes (basically, “countable” means you can label the numbers (like if you’re counting whole numbers 1, 2, 3…).
- A continuous joint distribution can be described by a non-negative function [1].
If the two variables are obtained through random sampling, you may be able to find correlations or run a regression analysis to investigate the link between the two variables or to predict future (or past) behavior of those variables.
Bivariate distributions are quite common in real life. For example:
- In an annual checkup, cholesterol levels and triglyceride levels might be combined to measure heart health.
- A gambler might want to know the probability of rolling a six, and then another six.
- A café might be interested in studying coffee sales vs. coffee cake sales.
- In transportation, the role of alcohol in car crashes is often investigated.
Table Representation of Bivariate Distribution
Unlike many probability distributions, a bivariate distribution doesn’t have a unified look; each distribution is different and it depends on what variables you are studying.
A table of rows and columns can be used to display discrete random variables with a finite (fixed) number of values. The rows represent one of the variables, the columns the other. For example, the following table shows the bivariate distribution of tossing a tails if you flip a coin three times:
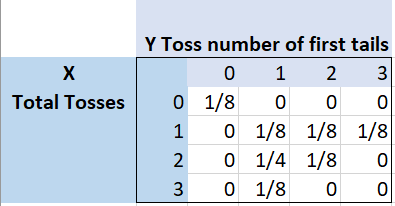
- The rows represent the X-values, which in this examples is the total number of tosses.
- The columns represent the Y-variable, which is the number of tosses to get the first tails (if no tails occur, this is set to zero).
- Each intersection represents an X-Y combination; the probabilities in those cells represent the joint probabilities.
As this is a probability distribution, the probabilities in all the cells add up to 1 [2].
References
[1] Liu, M. STA 611: Introduction to Mathematical Statistics; Lecture 4: Random Variables and Distributions. Retrieved November 10, 2021 from: http://www2.stat.duke.edu/courses/Fall18/sta611.01/Lecture/Lecture04.pdf
[2] Gehrman, J. 6. Bivariate Rand. Vars. Bivariate Probability Distributions. Retrieved November 10, 2021 from: https://www.csus.edu/indiv/j/jgehrman/courses/stat50/bivariate/6bivarrvs.htm