Power series distributions are discrete probability distributions on a subset of natural numbers. The distributions are named because they are constructed from the power series. Many discrete distributions fall under this general category of distributions including the binomial distribution, negative binomial distribution, and Poisson distribution.
A discrete random variable X has a power series distribution given as:
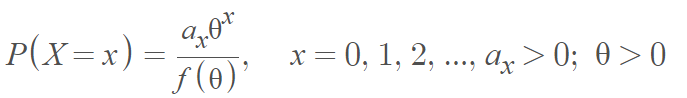
Where f(θ) is a generating function which is positive, finite, and differentiable [1].
The distribution is a member of the exponential family of distributions and can be expressed as follows [2]:
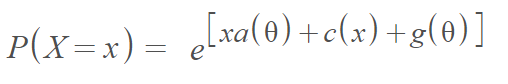
Where a and g are functions of θ, an unknown parameter and c is a function of x.
Special Properties of Power Series Distributions
The power series distribution has some special properties:
| Condition | Power Series Tends to… |
| If θ = p / (1 – p); f(θ) = (1 + θ)n; s = {1, 2, 3, … n} | Binomial distribution. |
| If f(θ) = eθ and s = {0, 1, 2, 3, … ∞} | Poisson Distribution. |
| If θ = p / (1 – p); f(θ) = (1 + θ)-n; s = {0, 1, 2, 3, … ∞} | Negative Binomial Distribution |
| If f(θ) = -log (1 – θ) and s = {1, 2, …}, | Logarithmic distribution |
Variations and Compounds of the Power Series Distribution
Several compounded distributions exist in the literature including the Weibull- power series distribution and the generalized Gompertz-power series distributions, obtained by compounding the generalized Gompertz distribution (a generalization of the exponential distribution) and the power series distributions [3].
Other variations include the exponential power series distribution, a composition of the exponential distribution with the power series distribution which gives a distribution with a decreasing failure rate [4].
References
[1] Gupta, R. (1974). Modified Power Series Distribution and Some of Its Applications. The Indian Journal of Statistics, Volume 36, Series B, Pt. 3, pp. 288-298.
[2] Sakia, R. (2018). Application of the Power Series Probability Distributions for the Analysis of Zero-Inflated Insect Count Data. Open Access Library Journal, Vol.5 No.10.
[3] Tahmasebi, S. & Jafari, A. (2000). Generalized Gompertz-Power Series Distributions. Retrieved December 14, 2021 from: https://www.academia.edu/25858978/Generalized_Gompertz-Power_Series_Distributions
[4] Chahkandi, M. & Ganjali, M. (2009). On some lifetime distributions with decreasing failure rate. Computational Statistics & Data Analysis 53(12): 4433-4440.