A univariate distribution is the probability distribution of a single random variable. For example, the energy formula (x – 10)2/2 is a univariate distribution because only one variable (x) is given in the formula. In contrast, bivariate distributions have two variables and multivariate distributions have two or more.
Types of Univariate Distribution
Hundreds of univariate distributions exist: some are more common than others. Many of these probability distributions are closely connected via transformations, some of which can be inverted. Transformations can include:
- Distribution of order statistic,
- Taking a mixture of random variables,
- Truncating random variables.
The following image shows how some of the major univariate distributions are connected. Discrete distributions are in blue; Continuous distributions are in green. Common sampling distributions are in orange.
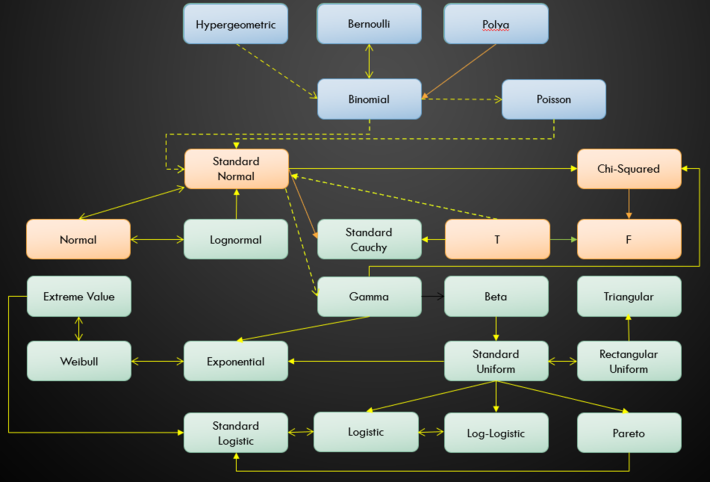
Discrete:
- Bernoulli Distribution: a discrete probability distribution for a Bernoulli trial — a random experiment with two outcomes (“Success” or a “Failure”).
- Beta binomial distribution: a mixture of a binomial and beta distribution.
- Binomial distribution
- Discrete uniform
- Gamma Poisson
- Hypergeometric
- Logarithm distribution
- Poisson distribution
- Polya distribution
- Power series
- Rectangular
- Zeta / Zipf
Continuous:
- Benford distribution
- Beta distribution
- Erlang
- Error distribution
- Extreme value
- Gamma (generalized)
- Gamma normal distribution
- Gompertz
- Hyperexponential distribution
- Kolmogorov Smirnov distribution
- Laplace
- Log logistic
- Log normal
- Logistic distribution
- Lomax
- Minimax distribution
- Muth distribution
- Noncentral beta distribution
- Normal Distribution
- Pareto distribution
- Rayleigh distribution
- Triangular
- Wald distribution
References
Leemis, L. & McQueston, J. Teacher’s Corner: Univariate Distribution Relationships. Retrieved February 19, 2021 from Academia.edu https://www.academia.edu/6823496/Univariate_Distribution_Relationships.
Univariate Distribution. Retrieved February 19, 2021 from: http://www.math.wm.edu/~leemis/chart/UDR/about.html