Johnson’s SB distribution is a system of curves for bounded data. The “SB” is short for “system bounded.”
Johnson [1] showed that a bounded random variable X (i.e., one with upper and lower limits) could be transformed to an approximately normal distribution with the transformation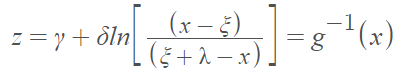
Where:
- ln = the natural logarithm,
- Z ~ N(0, 1) (i.e., a standard normal distribution with mean 0 and standard deviation 1).
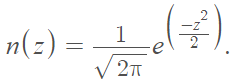
This leads to the equation for Johnson’s SB distribution:
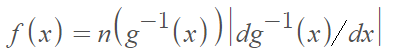
or
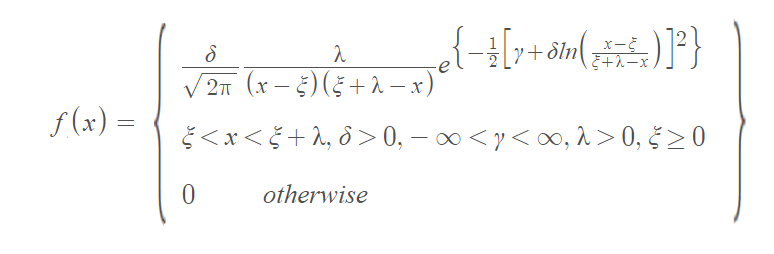
Olsson [2] explained the fitting of Johnson’s SB system and SU Systems of curves to grouped data using the method of maximum likelihood. This computer program Olsson developed uses the Nelder-Mead simplex subroutine and gives ML estimates for the four parameters required in the fitting procedure.
The SB distributions have the occasional practical application. For example, Hafley and Schreuder [3] introduced the distribution to the forestry literature. Several authors have expanded on the distribution in this field, including Parresol [4], who demonstrated recovery of parameters for the distribution.
References
[1] Johnson, N.L. 1949. Systems of frequency curves generated by methods of translation. Biometrika. 36: 149-176.
[2] Olsson, D. (1979). Fitting Johnson’s SB and SU Systems of Curves using the Method of Maximum Likelihood, Journal of Quality Technology, 11, 211-217.
[3] Hafley, W.L.; Schreuder, H.T. 1977. Statistical distributions for fitting diameter and height data in even-aged stands. Canadian Journal of Forest Research. 7: 481-487.
[4] Parresol, B. (2003). Recovering Parameters of Johnson’s SB distribution. USDA.