< Probability distributions < Bernoulli distribution
What is a Bernoulli Distribution?
A Bernoulli distribution is a discrete probability distribution for a Bernoulli trial — a random experiment that has only two outcomes (usually called a “Success” or a “Failure”). For example, the probability of getting a heads (a “success”) while flipping a coin is 0.5. The probability of “failure” is 1 – P (1 minus the probability of success, which also equals 0.5 for a coin toss).
It is a special case of the binomial distribution for n = 1. In other words, it is a binomial distribution with a single trial (e.g. a single coin toss).
The distribution is named after James Bernoulli (1654-1705), a Swiss mathematician who wrote the first major work on probability, called Ars Conjectandi (published posthumously in 1713) [1]. The book included details on the principles of counting and a proof of the binomial theorem [2]. The probability of a failure is labeled on the x-axis as 0 and success is labeled as 1. In the following Bernoulli distribution, the probability of success (1) is 0.4, and the probability of failure (0) is 0.6: 
Bernoulli Distribution Properties
Bernoulli distributions have several important properties:
- The probability of success is the same for each trial. If you flip a coin 100 times, 10 times or just once, the probability of getting a head on any given flip is the same: 0.5.
- The trials are independent: the result of one trial doesn’t affect the outcome of another. It doesn’t matter if you got heads or tails on the previous flips — it doesn’t affect the outcome of the next flip.
- The possible outcomes are binary, with two possible outcomes exist for each trial. If you flip a coin, the possible outcomes are “heads” and “tails.” For choosing a black ball from an urn with blue, black, red and green balls, the outcomes are “black” or “not black.”
The outcomes of a Bernoulli trial are called successes and failures. For example, if a coin lands on heads, it’s a “success” and if it lands on a tails, that’s a “failure.” However, that doesn’t mean an experiment is a failure in the usual sense of the word — it just means you didn’t get the result you were looking for in the experiment. For example, if you are counting whether frogs are present in ponds or not, and you come across a pond without a frog — then that’s a failure. A success in this case would be a pond with frogs. 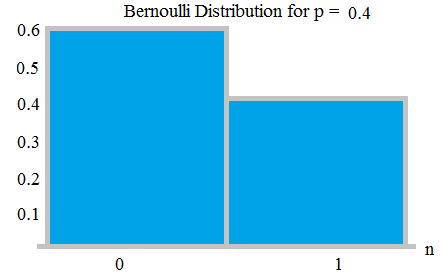The probability density function (pdf) for this distribution is px (1 – p)1 – x, which can also be written as: 
The probability of success is p and the probability of failure is q (q is sometimes written as 1 – p instead). These probabilities add up to 1:
p + q = 1
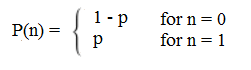
For example, let’s say the probability of you finding frogs in a pond is p = 0.4. The probability of a failure — not finding frogs — is q = 1 – 0.4 = 0.6. The expected value for a random variable, X, for a Bernoulli distribution is: E[X] = p. For example, if p = .04, then E[X] = 0.04. The variance of a Bernoulli random variable is: Var[X] = p(1 – p).
Bernoulli Trials explained
A Bernoulli trial is one of the simplest experiments you can conduct. It’s an experiment where there are two possible outcomes. A few examples:
- Coin Tossing – record how many coins land heads up or tails down?
- Births– what percent boys were born on any given day compared to girls (or vice versa)?
- Rolling Dice – does having more successes mean better luck for certain rolls as opposed to others?
Bernoulli trials are typically described in terms of success and failure. However, ‘success’ here doesn’t mean achievement in the traditional sense, but rather points to an outcome of interest. For example, if you want to know the daily number of boys born, a boy’s birth would be labeled as a ‘success’ while a girl’s birth would be labeled a ‘failure.’ Similarly, getting double sixes on a series of dice rolls could be a ‘success,’ while any other result would be a ‘failure.’
One of the most important aspects about Bernoulli trials is that each action must be independent. This means you cannot depend on what happened before, because it will affect your future outcomes — for example if I win a scratch off lottery ticket then my odds would change if I buy another ticket because one less winning ticket is on the market. Dependent events such as drawing lotto numbers come with different probabilities depending upon how many balls remain in play; when there are 100 left there is a 1/100th chance of drawing a certain numbered ball but when there are only ten balls left, the probability increases to 1/10.
Here are some examples of independent Bernoulli trials:
- Tossing a coin twice. The result of the first toss does not influence the outcome of the second toss.
- Rolling a die twice. The result of the first roll has no impact on the outcome of the subsequent roll.
- Drawing a card from a deck of cards twice. The result of the first draw does not influence the outcome of the next draw.
An example of a trial that isn’t independent (i.e., it’s dependent) is drawing two cards from a deck without replacing the first one. The outcome of the first draw influences the second because the deck now has one less card.
Bernoulli distribution vs. binomial distribution
A Bernoulli distribution is a special case of the binomial distribution with a one trial (e.g., the toss of one coin). In other words, the Bernoulli distribution is a special case of the binomial distribution with n = 1.
A binomial distribution tells us the probability of achieving a certain number of successful outcomes in a sequence of n Bernoulli trials. For example, the probability of flipping 5 heads in 10 coin flips can be represented by a binomial distribution. This means that while the Bernoulli distribution has 2 possible outcomes, the binomial distribution has 2n possible outcomes, because it can have any number of outcomes from 0 to n.
| Feature | Bernoulli distribution | Binomial distribution |
|---|---|---|
| Number of trials | 1 | n |
| Possible outcomes | 2 | 2n |
Is a coin flip binomial or Bernoulli?
Tossing a coin is an example of a Bernoulli trial, an experiment with only two potential outcomes, in this case, heads or tails. The Bernoulli distribution outlines the likelihood of achieving either heads or tails in a single coin flip. On the other hand, the binomial distribution gives us the probability of getting a specific number of successes (such as 5 heads) in a sequence of n Bernoulli trials. Therefore, flipping a coin once is a Bernoulli trial, not a binomial distribution because it involves only a single trial with two potential outcomes.
However, if you were to flip a coin 10 times, the distribution of the number of heads would follow a binomial distribution.
Is rolling a dice Bernoulli?
Rolling a die isn’t a Bernoulli trial.
That’s because a Bernoulli trial only has two possible outcomes. When you roll a die, six outcomes are possible (1, 2, 3, 4, 5, and 6). This is more than the two-outcome limit of a Bernoulli trial. However, if we define ‘success’ as rolling a specific number, such as 6, then rolling a die can be viewed as a Bernoulli trial as it now has two potential outcomes: rolling a 6 or not rolling a 6.
Therefore, while rolling a die is not typically a Bernoulli trial, it can be considered one if ‘success’ is defined in a particular manner.
What is a Bernoulli Trial?
A Bernoulli trial is one of the simplest experiments you can conduct. It’s an experiment where you can have one of two possible outcomes. For example, “Yes” and “No” or “Heads” and “Tails.” A few examples:
- Coin tosses: record how many coins land heads up and how many land tails up.
- Births: how many boys are born and how many girls are born each day.
- Rolling Dice: the probability of a roll of two die resulting in a double six.
Bernoulli trials are usually phrased in terms of success and failure. Success doesn’t mean success in the usual way—it just refers to an outcome you want to keep track of. For example, you might want to find out how many boys are born each day, so you call a boy birth a “success” and a girl birth a “failure.” In the dice rolling example, a double six die roll would be your “success” and everything else rolled would be considered a “failure.”
Independence
An important part of every Bernoulli trial is that each action must be independent. That means the probabilities must remain the same throughout the trials; each event must be completely separate and have nothing to do with the previous event. Winning a scratch off lottery is an independent event. Your odds of winning on one ticket are the same as winning on any other ticket. On the other hand, drawing lotto numbers is a dependent event. Lotto numbers come out of a ball (the numbers aren’t replaced) so the probability of successive numbers being picked depends upon how many balls are left; when there’s a hundred balls, the probability is 1/100 that any number will be picked, but when there are only ten balls left, the probability shoots up to 1/10. While it’s possible to find those probabilities, it isn’t a Bernoulli trial because the events (picking the numbers) are connected to each other. The Bernoulli process leads to several probability distributions:
The Bernoulli distribution is closely related to the Binomial distribution. As long as each individual Bernoulli trial is independent, then the number of successes in a series of Bernoulli trails has a Binomial Distribution. The Bernoulli distribution can also be defined as the Binomial distribution with n = 1.
Use of the Bernoulli Distribution in Epidemiology
In experiments and clinical trials, the Bernoulli distribution is sometimes used to model a single individual experiencing an event like death, a disease, or disease exposure. The model is an excellent indicator of the probability a person has the event in question.
- 1 = “event” (P = p)
- 0 = “non event” (P = 1 – p)
Bernoulli distributions are used in logistic regression to model disease occurrence.
References
- Bernoulli, J. (1713). Ars Conjectandi.
- Empirical Distributions