The location-scale family of distributions includes many popular distributions like the normal distribution and uniform distribution.
A random variable belongs to the location-scale family if its cumulative distribution
FX (x | a, b):= Pr(X ≤ | a, b) is a function only of (x – a)/b [1]:
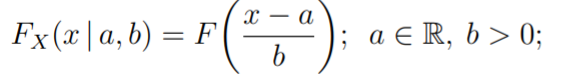
Where:
- F(·) is a distribution without any other parameters,
- a is a location parameter,
- b is a scale parameter.
If b = 1, the family is a location family, which is a subfamily of the location-scale family. If a = 0, the subfamily is a scale family with parameter b.
List of Location-Scale Family of Distributions
Many well-known statistical distributions belong to, or are closely related to, the location-scale family.
- Arcsine distribution,
- Cauchy distribution,
- Cosine distribution,
- Exponential distribution,
- Extreme value distributions,
- Half-Cauchy distribution,
- Half-logistic distribution,
- Half-normal distribution,
- Hyperbolic secant distribution,
- Laplace distribution,
- Logistic distribution,
- Maxwell-Boltzmann distribution,
- Normal distribution,
- Parabolic distributions of order 2,
- Rayleigh distribution,
- Semi–elliptical distribution,
- Teissier distribution,
- Triangular Distributions
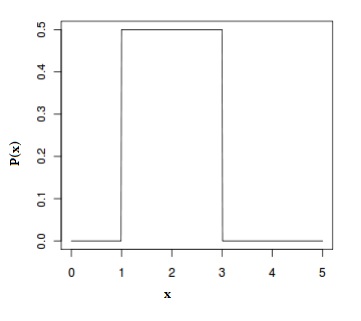
- Uniform or rectangular distribution,
- U–shaped and inverted U–shaped distributions,
- V–shaped distributions.
Several other distributions have special cases that belong to the family, including the beta distribution, chi-distribution, and power–function distribution. As an example, the four parameter beta distribution isn’t in the scale-location family because it has two “extra” parameters, c and d. However, if both c and d are set to 1, the distribution becomes the uniform distribution — which is a “true” member of the location-scale family.
Other distributions can be transformed or otherwise tweaked to join the family. For example, an exponential distribution that is reflected over the x-axis at x = a will be a location-scale distribution.
Log-Location Scale Family
A related family is the log-location scale family, which includes the lognormal distribution, the loglogistic distribution, and the Weibull distribution. A distribution is in the log-location scale family if Y = log(T) is a member of the location-scale family [2].
References
[1] The family of location–scale distributions. Retrieved December 15, 2021 from: http://geb.uni-giessen.de/geb/volltexte/2010/7607/pdf/RinneHorst_LocationScale_2010.pdf
[2] Location-Scale-Base Parametric Distributions.