What is a Fat Tail Distribution?
The term “fat tail” distribution has more than one definition, depending on where you read about it. Part of the problem is that there’s no universal definition for the term tail in the first place (does it begin at 2 standard deviations from the mean? A little bit left or right of the peak?).
Another issue is that the term “fat tail distribution” has been adopted by many non-mathematicians and lay authors to mean “a probability distribution with a tail that looks fatter than usual.” Part of the reason for that is it’s probably much easier for the non-statistician to visualize what a fat tail is, as opposed to a heavy one. A second part of the reason is that if you’re simply being descriptive, “fat tail” is a good descriptor (along with “tall, thin peak” or “short and fat”), albeit not a mathematically precise one.
- As a synonym for a heavy tailed distribution.
- As a synonym for Leptokutric.
- To describe a subset of heavy tailed distributions.
1. As a synonym for heavy tailed distribution
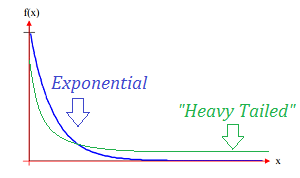
A heavy tailed distribution has tails that are heavier than an exponential distribution (Bryson, 1974). In other words, the tails simply look fatter. As the tails have more bulk, the probability of extreme events is higher compared to the normal. This definition, where “heavy tail” and “fat tail” mean the same thing, is especially common in trading and other areas of finance.
Fat tail distributions has a much greater chance of values above 4 or 5 standard deviations. As a result of this, finding an event at 8 standard deviations from the mean in a normal distribution is a near impossible event (6 x 10-16), while in the fat tail distribution, the probability of the same event is 4%, i.e., it will happen about once in every 25 events (Neto, 2014).
For examples, see: What is a Heavy Tailed Distribution?
2. As a Synonym for Leptokurtic
A leptokurtic distribution has excess positive kurtosis. The tails are “fatter” than the normal distribution, hence the term fat-tailed.
3. To Describe a sublclass of heavy tailed distributions
Some authors reserve the term “fat tail” to mean the subclass of heavy tailed distributions that exhibit power law decay behavior as well as infinite variance. For example, Taylor (2016) defines a distribution X with a fat right tail as one with a positive exponent α (called the tail index) so that
P(X > x) ∼ x−α
As x → ∞
Every fat-tailed distribution is heavy tailed, although with this in mind, not every heavy tailed distributiuon has a fat tail. For example, the Weibull distribution is heavy-tailed but not fat-tailed.
References
Bryson, M. (1974). Heavy Tailed Distributions: Properties and Tests. Technometrics 16(1):61-68 (February 1974).
Neto, J. (2014). Power Laws and Heavy Tailed Distributions. Retrieved December 10, 2017 from: http://www.di.fc.ul.pt/~jpn/r/powerlaw/powerlaw.html
Taylor, J. (2016). Heavy-tailed Distributions. Retrieved December 10, 2017 from: https://math.la.asu.edu/~jtaylor/teaching/Spring2016/STP421/lectures/stable.pdf