Probability Distributions > Generalized Error Distribution / Generalized Normal
What is a Generalized Error Distribution?
Generalized error distributions (sometimes called generalized normal distributions) are a symmetric family of distributions used in mathematical modeling, usually when errors (the difference between the expected value and the observed values) aren’t normally distributed. Special cases of this distribution are identical to the normal distribution and the Laplace distribution.
The Generalized error distribution is useful when the errors around the mean or in the tails are of special interest. If other deviations from the normal distribution are being studied, other families of distributions can be used. For example, the t-distribution is used if the tails are of interest; the t-distribution approximates the normal distribution as degrees of freedom in the distribution approach infinity.
Three parameters define the distribution:
- The mean, μ, which determines the mode (the peak) of the distribution. Like the standard normal distribution, the median and mode are equal to μ.
- The standard deviation, σ, which determines the dispersion.
- A shape parameter, Β. Some authors refer to this as kurtosis, as kurtosis tells you how much data is in the tails (which in turn, tends to give you some information about the peak).
A generalized normal distribution with Β = 1/2 is equal to the normal distribution; if Β = 1 it is equal to the Double Exponential or Laplace distribution. For values of Β that tend toward zero, the distribution starts to look like a uniform distribution.
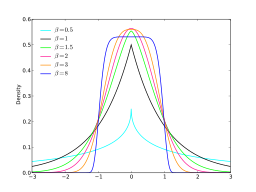
Classes of the Generalized Error Distribution
The two classes of the Generalized Error Distribution have heavy tails or highly skewed tails. Statisticians R. Vasudeva and J. Vasanthat Kumari describe these classes as:
- Generalized Error Distributions of the first kind (GED-1). This class has heavy tails.
- Generalized Error Distributions of the second kind (GED-2). This class has highly skewed tails.