The Gompertz-Makeham distribution (also called the Makeham distribution) is a continuous probability distribution used in insurance to model the lifetimes of adults. The distribution, used to create actuarial tables, is based on analytical laws of mortality developed by Benjamin Gompertz and William Makeham. Gompertz’s 1825 paper, where he hypothesized that the probability of dying increases in geometrical progression, marked an “epoch in the history of actuarial science” [1].
The Gompertz–Makeham distribution is the basis for the Gompertz–Makeham law of mortality, which states the death rate for humans can be calculated with two components: one age-dependent and one age-independent.
PDF of the Gompertz-Makeham Distribution
The probability density function is:
![]()
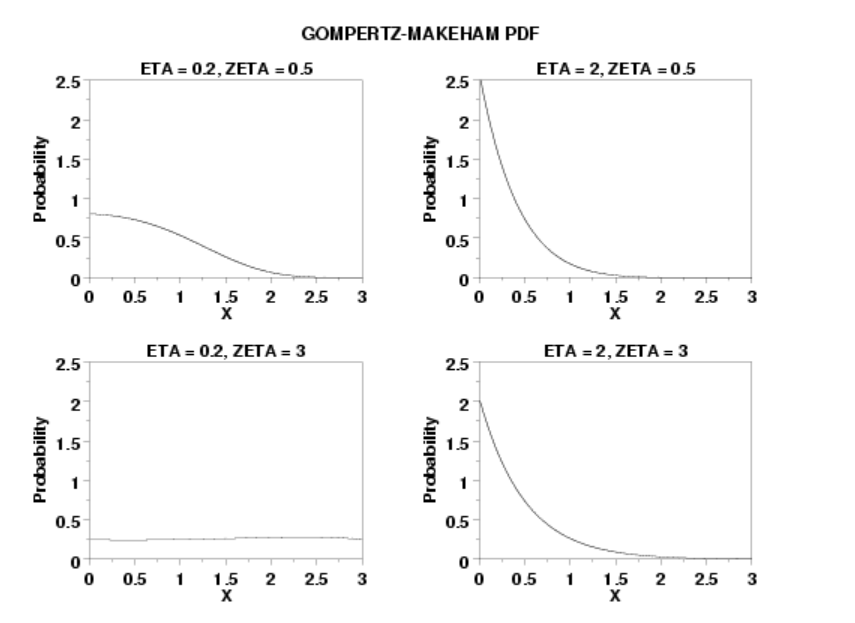
The distribution is defined over the interval [0, ∞] and can take on a wide variety of shapes: The PDF may be unimodal, or in some cases monotonically decreasing with a singularity as x approaches zero. The distribution can also be fat tailed (decreases algebraically) or thin tailed (decreases exponentially), depending on the parameters [2]:
- γ = shape parameter.
- δ = frailty parameter.
Note that “frailty” here doesn’t refer to individuals, but rather populations. More specifically, it is an unobservable univariate statistical variable Z that describes a relationship with the “force of mortality” [3].
The Gompertz distribution is a special case of the Gompertz-Makeham distribution when γ = 0 [4].
Gompertz Function
The Gompertz function, the building block for the Gompertz-Makeham distribution as well as many other life distributions [5], is expressed as:
Rm = R0 eat,
Where:
- Rm = mortality rate,
- a and R0 = constants,
- t = time parameter.
References
Image: NIST. Retrieved November 15, 2021 from: https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/makpdf.htm
[1] Henderson, A. (1968). Actuarial methods for estimating morality parameters of industrial property.
[2] GompertzMakehamDistribution. Retrieved November 15, 2021 from: https://reference.wolfram.com/language/ref/GompertzMakehamDistribution.html
[3] Butt, Z. & Haberman, S. Application of Frailty-Based Mortality Models using Generalized Linear Models.
[4] Leemis. Theorem. Retrieved November 15, 2021 from: http://www.math.wm.edu/~leemis/chart/UDR/PDFs/MakehamGompertz.pdf
[5] [Gompertz, 1825] as cited in Norström, F. The Gompertz-Makeham distribution. Retrieved November 15, 2021 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1068.8330&rep=rep1&type=pdf