Descriptive Statistics > Symmetric Distribution
A symmetric distribution is a type of distribution where the left side of the distribution mirrors the right side. A symmetric distribution is never skewed .
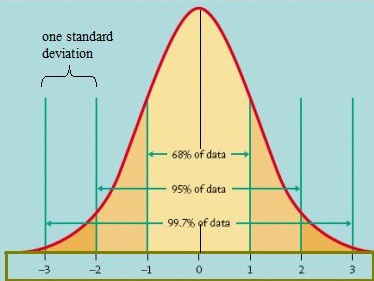
The normal distribution is symmetric. It is also a unimodal distribution (it has one peak).
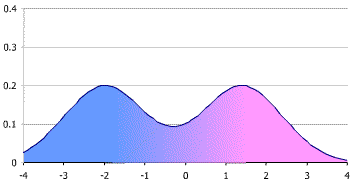
Distributions don’t have to be unimodal to be symmetric. They can be bimodal (two peaks) or multimodal (many peaks). The following bimodal distribution is symmetric, as the two halves are mirror images of each other.
Mean, Mode and Median of a Symmetric Distribution
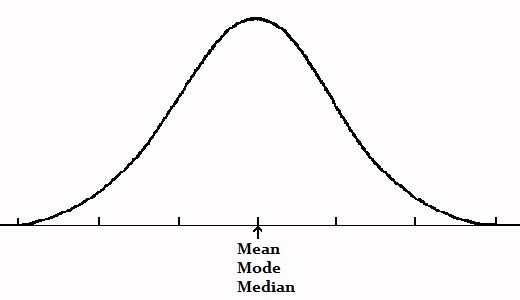
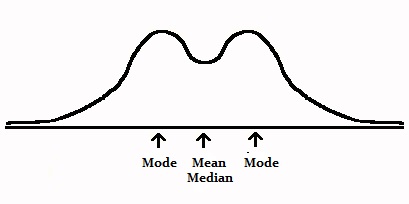
In a symmetric distribution, the mean, mode and median all fall at the same point. The mode is the most common number and it matches with the highest peak (the “mode” here is different from the “mode” in bimodal or unimodal, which refers to the number of peaks).
An exception is the bimodal distribution. The mean and median are still in the center, but there are two modes: one on each peak.
Other Symmetric Distributions
The normal distribution is the symmetric distribution you’re most likely to come across in elementary statistics. However, there are other distributions that display symmetry:
- The bimodal distribution can be symmetrical if the two peaks are mirror images.
- Cauchy distributions have symmetry. You’re unlikely to come across these in elementary stats. They are a family of distributions where the expected value doesn’t exist.
- The logistic distribution, which has long tails. The logistic and Cauchy distributions are used if the data is symmetric but there are more extreme values than you would expect to find in a normal distribution. Read more about these distribution types here.
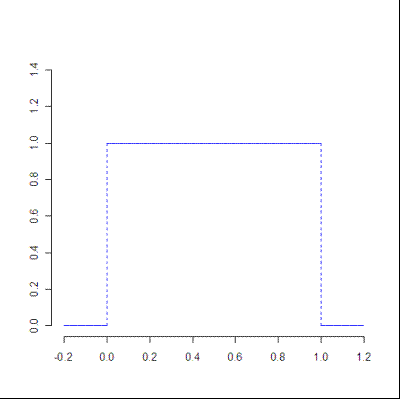
- The uniform distribution is symmetric. The probabilities are exactly the same at each point, so the distribution is basically a straight line. An example of a uniform probability distribution could be picking a card from a deck: the probability of picking any one card is the same: 1/52.

Uniform distribution. Image courtesy of the University of Houston.
References
Fang, K. (2018). Symmetric Multivariate and Related Distributions. Chapman & Hall/CRC.