The power function distribution is a flexible model often used for the analysis of income distribution data, lifetime data, and modeling of failure processes. For example, one use of the distribution is in reliability assessment of electrical components and semiconductor devices [1]. One strength of the power function distribution is its mathematical simplicity, compared to more complex distributions like the Weibull distribution.
Theoretically, the power function distribution is a special case of the beta distribution [2], and the Pearson type I distribution. It also has an inverse relationship with the standard Pareto distribution [3]; moments of the power function distribution are the negative moments of the Pareto distribution [4].
Power-Function Distribution PDF
A random variable has a power function distribution if its PDF is [5]:
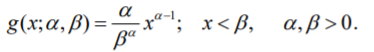
Note on “Power Functions”
A power function has the form f(x) = axp. There are an infinite number of possible power functions, depending on your choice of scaling factor a and exponent p. Each power function has an associated distribution (or graph). Therefore, the term power function distribution could refer to one of these distributions (rather than “the” power function distribution described above).
References
[1] Sultan K, Childs A, Balakrishnan N. Higher order moments of order statistics from the power function distribution and Edgeworth approximate inference. Advances in Stochastic Simulation Methods Springer. 2000; 245–282.
[2] Pandey, A. & Saran, J. (2004). ESTIMATION OF PARAMETERS OF A POWER FUNCTION DISTRIBUTION AND ITS CHARACTERIZATION BY K-TH RECORD VALUES. STATISTICA, anno LXIV, n.3. Retrieved December 6, 2021 from: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.953.5181&rep=rep1&type=pdf
[3] Kleiber C, Kotz S. Statistical size distributions in economics and actuarial sciences: John Wiley & Sons; 2003.
[4] Johnson NL, Kotz S. Distributions in Statistics: Continuous Univariate Distributions: Vol 1. John Wiley & Sons; 1970.
[5] Ansari, S. et al. (2019). Cubic Transmuted Power Function Distribution. Gazi University Journal of Science. 32(4): 1322-1337. Retrieved December 16, 2021 from: https://scholar.ppu.edu/bitstream/handle/123456789/2026/2019_Cubic%20Transmuted%20Power%20Function%20Distribution.pdf?sequence=1&isAllowed=y