The arcsine distribution and the generalized arcsine distribution are found in the study of random walk fluctuation, renewal theory, and as the Jeffrey’s prior for successes in a Bernoulli trial. The generalized arcsine distribution, used in mathematical statistics, is a special case of the beta I distribution, when a = b = ½.
It’s called the arcsine distribution because “arcsin x” is the arc that has a sine of x.
Although the distribution is used in some fairly weighty mathematical areas, a simple example of what the distribution can be used for is as the fraction of time a player can win a coin toss game, assuming the coins are fairly weighted (Rasnick, 2019).
PDF for the Arcsine Distribution
The probability density function (PDF) of the standard arcsine distribution is defined as:
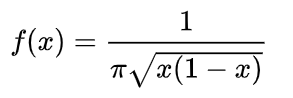
The PDF is supported for an interval of between 0 and 1 (0 < 1). Outside of this boundary, the density is zero. The distribution can be generalized to include any bounded support between two values a and b, or by using scale parameters and location parameters.
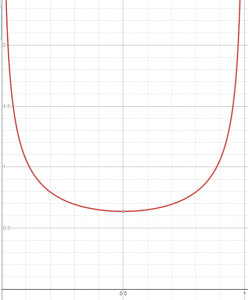
The PDF of the arcsine distribution is U-shaped:
CDF for the Arcsine Distribution
The cumulative distribution function (CDF) for the arcsin function is:
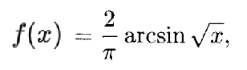
The CDF is valid for x-values from 0 to 1 (0 < x < 1); The CDF is concentrated near the boundary values 0 and 1. As the distribution gets very close to 1, it tends to infinity. It includes the inverse sin (arcsin), which is where the distribution gets its name.
References
Agrawal, N. et al. Arcsin Distribution. Retrieved January 21, 2020 from: https://www.boost.org/doc/libs/1_58_0/libs/math/doc/html/math_toolkit/dist_ref/dists/arcine_dist.html
Balakrishnan, N. & Nevzorov, V. (2004). A Primer on Statistical Distributions. John Wiley & Sons.
Hazewinkel, M. (1994). Encyclopaedia of Mathematics (set). Springer Science & Business Media.
Mörters, P. & Peres, Y. (2010). Brownian Motion. Cambridge University Press.
R-forge distributions Core Team. (2009-2010). Handbook on probability distributions. Retrieved January 21, 2020 from: http://www.stat.rice.edu/~dobelman/textfiles/distributions.r-forge.pdf
Rasnick, Rebecca, “Generalizations of the Arcsine Distribution” (2019). Electronic Theses and Dissertations. Paper 3565. https://dc.etsu.edu/etd/3565