Negative Binomial Experiment / Distribution: Definition, Examples

Binomial Theorem > Negative Binomial Experiment Contents:

1. Negative Binomial Experiment
2. Negative Binomial Distribution

 

1. Negative Binomial Experiment

The negative binomial experiment is almost the same as a binomial experiment with one difference: a binomial experiment has a fixed number of trials. If the following five conditions are true the experiment is binomial:

1. Fixed number of n trials.
2. Each trial is independent.
3. Only two outcomes are possible (Success and Failure).
4. Probability of success (p) for each trial is constant.
5. A random variable Y= the number of successes.

Example: Take a standard deck of cards, shuffle them, and choose a card. Replace the card and repeat twenty times. Y is the number of aces you draw. The negative binomial is similar to the binomial with two differences (specifically to numbers 1 and 5 in the list above):

• The number of trials, n is not fixed.
• A random variable Y= the number of trials needed to make r successes.

Example: Take a standard deck of cards, shuffle them, and choose a card. Replace the card and repeat until you have drawn two aces. Y is the number of draws needed to draw two aces. As the number of trials isn’t fixed (i.e. you stop when you draw the second ace), this makes it a negative binomial distribution.

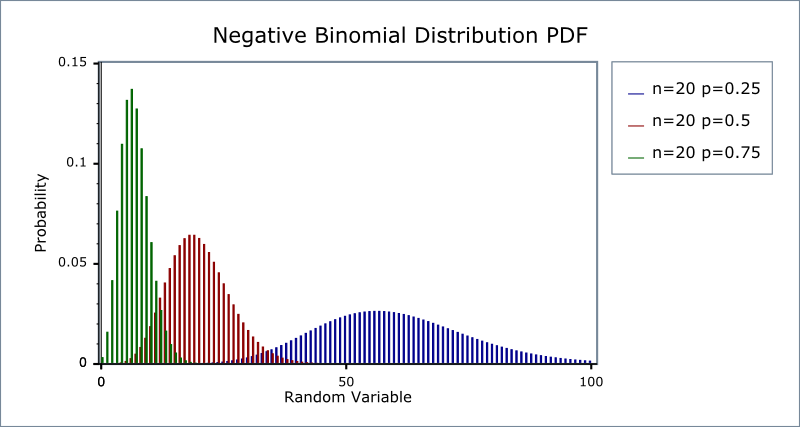
2. Negative Binomial Distribution

A negative binomial distribution (also called the Pascal Distribution) is a discrete probability distribution for random variables in a negative binomial experiment. It is used when there are exactly two mutually exclusive outcomes, labelled “success” and “failure”. The random variable is the number of repeated trials, X, that produce a certain number of successes, r. In other words, it’s the number of failures before a success. This is the main difference from the binomial distribution: with a regular binomial distribution, you’re looking at the number of successes. With a negative binomial distribution, it’s the number of failures that counts. A negative binomial experiment must meet the following requirements [1]:

1. 1. The experiment must consist of a sequence of independent trials.

1. 1. Each trial results in a success (S) or failure (F).

1. 1. The probability of success is the same from trial to trial.

1. 1. The experiment continues until you have r successes, where r is a positive integer (i.e., 1, 2, 3, …).

In addition, the name “negative binomial distribution” is often used only when the success parameter r is an integer. This integer version also goes by the name the Pascal distribution [2].

Why is it called Negative Binomial?

When you hear the term negative, you might think that a positive distribution is flipped over the x-axis, making it negative. However, the “negative” part of negative binomial actually stems from the fact that one facet of the binomial distribution is reversed: in a binomial experiment, you count the number of Successes in a fixed number of trials; in the above example, you’re counting how many aces you draw. In a negative binomial experiment, you’re counting the Failures, or how many cards it takes you to pick two aces.

Formula

Probability: b*(x; r, P) = _x-1C_r-1 * P^r * (1 – P)^{x – r} where x=number of trials r = Successes Mean: μ = r / P where r is the number of trials P=probability of success for any trial

Solving Negative Binomial Experiment Problems

The probability mass function (pmf) for the negative binomial distribution is:
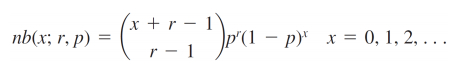
Where: r is the number of successes and p = the probability of success. Example question 1: You are surveying people exiting from a polling booth and asking them if they voted independent. The probability (p) that a person voted independent is 20%. What is the probability that 15 people must be asked before you can find 5 people who voted independent? Step 1: Find p, r and X. We are given (in the question) that p = 20%(.2) and r = 5. The number of failures, X, is 15 – 5 = 10. Step 2: Insert those values from Step 1 into the formula:
Step 3: Solve. The first part (14 over 4) is a combination (use our combinations calculator to find 14 choose 4). 1001*.2⁵*.8¹⁰ = 0.034. The probability you’ll have to ask 15 people to get 5 votes for independent is .034, or 3.4%. Example question 2: you are running a weight loss experiment and need 5 people willing to participate who have never tried a weight loss program before. If the probability that a randomly selected person has never tried a weight loss regimen is 0.2, what is the probability you must ask 15 people before you can find 5 people who have never tried losing weight? Solution: Place the following information into the formula:

• • r = 5 (number of successes = people who have never tried losing weight)

• • x = 10 (number of failures = people who have tried losing weight)

• • p = 0.2 = probability of success.

The probability is 3.4% that you will find 5 candidates from 15 people. The geometric distribution is a special case of the negative binomial distribution when r = 1. The Poisson distribution is a special case when the number of successes is very large (i.e. tends to infinity).

References

[1] 3.5 Hypergeometric and Negative Binomial Distributions. Retrieved September 1, 2023 from: https://www.stat.purdue.edu/~zhanghao/STAT511/handout/Stt511%20Sec3.5.pdf [2] Boost C++ libraries. Negative Binomial Distribution. Retrieved September 1, 2023 from: https://valelab4.ucsf.edu/svn/3rdpartypublic/boost/libs/math/doc/sf_and_dist/html/math_toolkit/dist/dist_ref/dists/negative_binomial_dist.html