What is the Robust Soliton Distribution?
Analysis of LT (Luby transform) codes is based on the analysis of the decoding algorithm, the LT processes. Each LT code symbol is generated by randomly selecting the degree of the code symbol, d, between 1 and k. The Robust Soliton distribution is a degree distribution, a way to construct a good degree of encoding symbols [1]. The distributed is constructed so that the decoder can recover data from slightly more than k code symbols with probability > 1 – δ, where δ is between 0 and 1 [2].
The distribution is used in coding theory, specifically in the theory of erasure correcting codes. It uses information redundancy to compensate for transmission errors presenting as missing data.
Formulas of Ideal and Robust Soliton Distribution
Liby [2] introduced two distributions, the ideal soliton distribution and the robust soliton distribution.
The ideal soliton distribution, is defined as a probability distribution with a single parameter K:
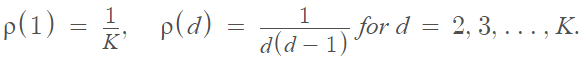
optimizes the expected probability that there is a decodable source block at each iteration of the process. However, there is an unacceptable probability of failing at some iteration. This issue can be addressed with the robust soliton distribution, which adds an extra set of values [3]:
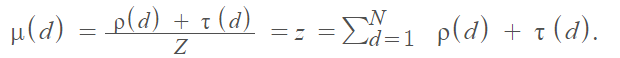
The ideal soliton distribution has a peak at 2, while the extra component in the robust distribution adds an additional peak at the value K/R.
References
[1] Project 5: Capstone Project: LT Codes. Retrieved July 14, 2021 from: http://cs.brown.edu/courses/csci1680/f17/content/lt.pdf
[2] Luby, M. (2002). LT Codes, Proc. of the 43rd Annual IEEE Symp. on Foundations of Comp. Sc., pp 271-280, Vancouver, Canada, November.
[3] Joshi et al. Fountain Codes. Retrieved July 14, 2021 from: https://www.andrew.cmu.edu/user/gaurij/FountainCodes.pdf