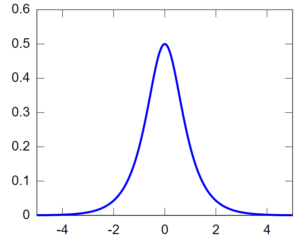
The Hyperbolic Secant distribution is a bell-shaped, symmetric member of the exponential family with a mean of 0 and variance of 1. It is a continuous distribution that is tractable, which means calculation of the distribution at any point takes polynomial-time.
Hyperbolic Secant Distribution PDF
A random variable X = ln|Y1/Y2| follows a hyperbolic secant distribution (where Y are normal random variables). The density of the distribution is proportional to the hyperbolic secant function, the reciprocal of the hyperbolic cosine function defined by [1]:
cosh(x) = 0.5 [ex + e-x]
The probability density function of the hyperbolic secant is [2]:
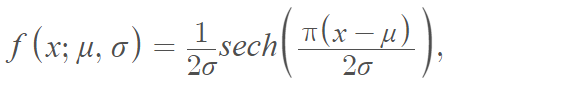
Where μ ∈ ℝ and σ > 0 and
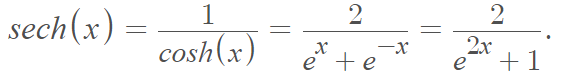
The sample mean and sample median are equally efficient estimators for the population distribution.
The Hyperbolic Secant distribution is not as well known as other exponential family distributions due to its isolation from many well known statistical models [3]. It does bear some similarities to the normal distribution both in shape and symmetry. Both distributions have a density proportional to their characteristic functions although the hyperbolic secant has slightly heavier tails [4].
References
Top Image: IkamusumeFan,
[1] Stat 5601 (Geyer) Hyperbolic Secant Distribution. Retrieved December 18, 2021 from: https://www.stat.umn.edu/geyer/old02/5601/examp/hsec.html
[2] Rubio, F. The Hyperbolic Secant Distribution. Retrieved December 18, 2021 from: https://rpubs.com/FJRubio/HSD
[3] Ding, P. (2014). Three Occurrences of the Hyperbolic-Secant Distribution. Retrieved December 18, 2021 from: https://arxiv.org/abs/1401.1267
[4] M. J. Fischer, Generalized Hyperbolic Secant Distributions, 1
SpringerBriefs in Statistics, DOI: 10.1007/978-3-642-45138-6_1