The noncentral beta distribution is a generalization of the Beta Distribution. The Beta distribution, although useful in many ways, has a significant drawback: it cannot properly model portions of data that have values next to zero and one [1]. The noncentral beta distribution overcomes this drawback. Some practical applications of the distribution include:
- Modeling single wave propagating across a receiver array with added Gaussian noise [2].
- Estimating coil sensitivity profiles in magnetic resonance image reconstruction [3].
Noncentral Beta Distribution PDF
A noncentral beta distribution has a probability density function of
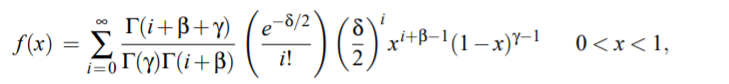
Where:
- β and γ are positive shape parameters,
- δ is a positive noncentrality parameter.
In general, the PDF is unimodal with a single peak.
The noncentral beta distribution has some strong limitations in
terms of interpretability and tractability. For any random variable X with a noncentral beta distribution, the following are mathematically intractable [4]:
- Cumulative distribution function,
- Survivor function,
- Hazard and cumulative hazard function,
- Inverse distribution,
- Moment generating function,
- Characteristic functions,
- Population mean,
- Population variance,
- Skewness,
- Kurtosis.
Note that intractable means difficult or hard, not “impossible.” There are ways to calculate them, although they are complicated. For example, the CDF can be calculated with various algorithms, the simplest of which is based on a sharp error bound [5]. A FORTRAN77 library is also available to evaluate the CDF [6].
References
[1] Orsi, C. (2017). New insights into non-central beta distributions. Retrieved November 29, 2021 from: https://arxiv.org/pdf/1706.08557.pdf
[2] Kimball, C.V., Scheibner, D.J.: Error bars for sonic slowness measurements. Geophysics, 63, 345–353, (1998)
[3] Stamm, A., Singh, J., Afacan, O., Warfield, S. K.: Analytic quantification of biasand variance of coil sensitivity profile estimators for improved image reconstructionin MRI. Medical Image Computing and Computer-Assisted Intervention MICCAI
2015, 684–691 (2015)
[4] Noncentral beta distribution. Retrieved November 29, 2021 from: http://www.math.wm.edu/~leemis/chart/UDR/PDFs/Noncentralbeta.pdf
[5] Chattamvelli, R. A Note on the Noncentral Beta Distribution Function. Retrieved November 29, 2021 from: https://www.jstor.org/stable/2684647
[6] ASA226 CDF of the noncentral Beta Distribution. Retrieved November 29, 2021 from: https://people.math.sc.edu/Burkardt/f77_src/asa226/asa226.html