Contents:
What is a Logarithmic Distribution?
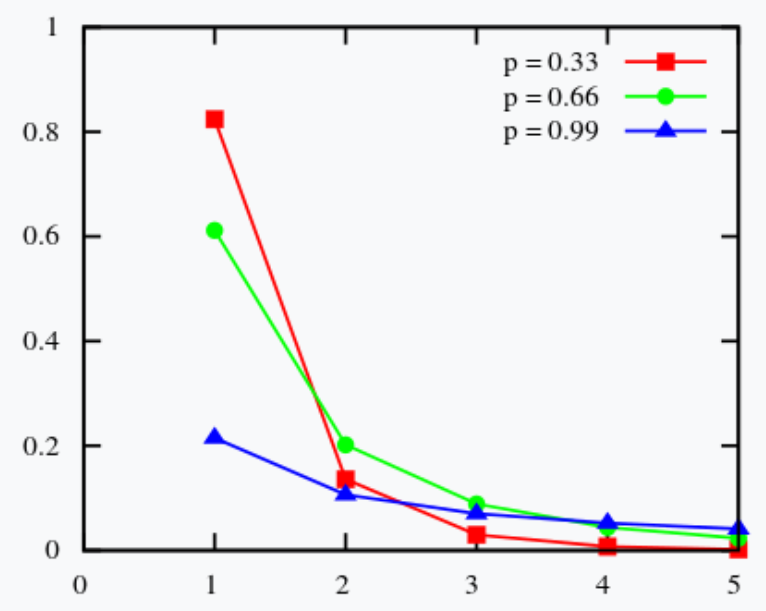
The logarithmic distribution (also called the logarithmic series distribution or log-series distribution) is a discrete probability distribution derived from the Maclaurin series expansion. It has one parameter β, which ranges from 0 to 1, and a long right tail. The distribution is used to model a wide range of phenomena from insurance claim frequency to species diversity data. For example, Fisher, Corbet, and Williams used the log-series distribution in 1943 to sample butterflies and obtain data for moths in a light trap [1].
A random variable with this distribution can be denoted as X ~ Log(p); the RV has the probability mass function of [2]:
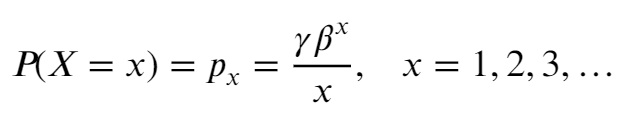
Where γ = -1/ln(1 – β).
A modified version called the logarithmic-with-zeroes-distribution was introduced in 1957 by Williams [3]; it allows for zeros and has the probability generating function (PGF):
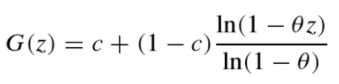
Other “Logarithmic Distribution” Types
Sometimes, the term “logarithmic distribution” refers to any distribution that involves logarithms. For example, the lognormal distribution, obtained from the normal distribution via a transformation, is called a logarithmic distribution in the Springer Series in Statistics Life Distributions [4].
Another variant found in the literature is the “logarithm distribution”, which has a slightly different form of the Probability Mass Function.
The logarithm distribution is a discrete probability distribution with outputs that decrease drastically as x-values increase. The distribution is defined only for integer values x = 1, 2, 3, …. Both of the factors mean that the distribution has limited real-life uses for model fitting, but some natural phenomena that experience a rapid decline may fit a logarithmic model.
The probability mass function is:
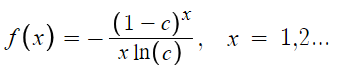
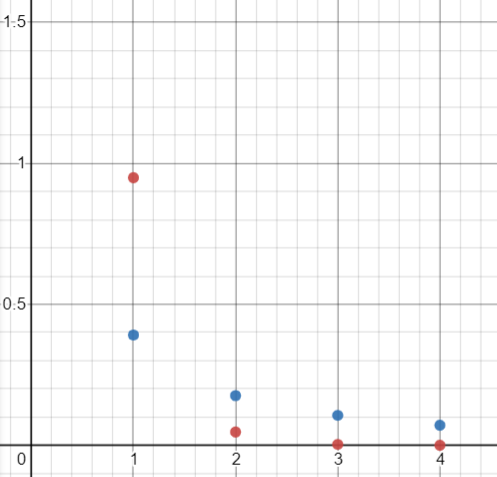
X ∼ logarithm(c) indicates a random variable X has a logarithm distribution with parameter c.
References
PMF Image: Qwfp,
[1] : R. A. Fisher, A. Steven Corbet, C. B. Williams. The Relation Between the Number of Species and the Number of Individuals in a Random Sample of an Animal Population. The Journal of Animal Ecology, Vol. 12, No. 1 (May, 1943), pp. 42-58. Retrieved November 15, 2021 from: https://www.math.mcgill.ca/dstephens/556-2008/Papers/Fisher1943.pdf
[2] D. J. Best, J. C. W. Rayner, O. Thas, “Tests of Fit for the Logarithmic Distribution”, Advances in Decision Sciences, vol. 2008, Article ID 463781, 8 pages, 2008. https://doi.org/10.1155/2008/463781
[3] Johnson, N. Kemp, A. Kotz, S. (2005). Univariate Discrete Distributions. Wiley.
[4] Marshall A.W., Olkin I. (2007) Logarithmic Distributions. In: Life Distributions. Springer Series in Statistics. Springer, New York, NY. https://doi.org/10.1007/978-0-387-68477-2_12