Probability Distributions > Exponential Distribution
Contents:
- What is an Exponential Distribution?
- What is a Poisson Process?
- Uses in real life
- Memoryless Property
- Exponential PDF
- Exponential CDF
- Connection to other distributions
- Exponential Family
What is an Exponential distribution?
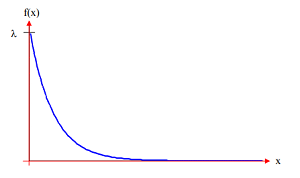
There is a strong relationship between the Poisson distribution and the Exponential distribution. For example, let’s say a Poisson distribution models the number of births in a given time period. The time in between each birth can be modeled with an exponential distribution (Young & Young, 1998).
What is a Poisson Process?
The Poisson process gives you a way to find probabilities for random points in time for a process. A “process” could be almost anything:
- Accidents at an interchange.
- File requests on a server.
- Customers arriving at a store.
- Battery failure and replacement.
The Poisson process can tell you when one of these random points in time will likely happen. For example, when customers will arrive at a store, or when a battery might need to be replaced. It’s basically a counting process; it counts the number of times an event has occurred since a given point in time, like 1210 customers since 1 p.m., or 543 files since noon. An assumption for the process is that it is only used for independent events.
Poisson Process Example
Let’s say a store is interested in the number of customers per hour. Arrivals per hour has a Poisson 120 arrival rate, which means that 120 customers arrive per hour. This could also be worded as “The expected mean inter-arrival time is 0.5 minutes”, because a customer can be expected every half minute — 30 seconds.
The negative exponential distribution models this process, so we could write:
Poisson 120 = Exponential 0.5
So the units for the Poisson process are people and the units for the exponential are minutes.
The 120 customers per hour could also be broken down into categories, like men (probability of 0.5), women (probability of 0.3) and children (probability of 0.2). You could calculate the time interval between the arrivals times of women, men, or children.
For example, the time between arrivals of women would be:
A rate 0.3*120 = 36 per hour, or one every 100 seconds.
For men it would be:
A rate of 0.5*120 = 60 per hour, or one every minute.
And for children:
A rate of 0.2*120 = 24 per hour, or one every 150 seconds.
What is the Exponential Distribution used for?
The exponential distribution is mostly used for testing product reliability. It’s also an important distribution for building continuous-time Markov chains. The exponential often models waiting times and can help you to answer questions like:
- “How much time will go by before a major hurricane hits the Atlantic Seaboard?” or
- “How long will the transmission in my car last before it breaks?”.
If you assume that the answer to these questions is unknown, you can think of the elapsed time as a random variable with an exponential distribution as long as the events occur continuously and independently at a constant rate.
Back to top
Memoryless Property
This distribution has a memoryless property, which means it “forgets” what has come before it. In other words, if you continue to wait, the length of time you wait neither increases nor decreases the probability of an event happening. Any time may be marked down as time zero. Let’s say a hurricane hits your island. The probability of another hurricane hitting in one week, one month, or ten years from that point are all equal. The exponential is the only distribution with the memoryless property.
While many authors consider the memoryless property to be one of the most useful aspects of the distribution, it’s also the reason why it may not make sense for modeling certain situations. For example, let’s say you wanted to model deaths of family dogs. Because of the memoryless property, the probability of a pet dog dying at age 1 would be the same as the dog dying at age 15, which is obviously nonsensical. Therefore, you should think about whether the exponential makes sense logically to your particular area of interest. For lifetime studies, the exponential is usually used only as a first rough model for the process.
Probability Density Function
The most common form of the pdf is:
F(x;λ) = e-λx x > 0.
Where:
- e = the natural number e,
- λ = mean time between events,
- x = a random variable.
For x less than 0, F(x;λ) = 0
An alternate form of the pdf [1] is:
f(x) = (1/β) e − (x − μ) / β x ≥ μ ; β > 0
where μ is the location parameter and β is the scale parameter. The scale parameter is sometimes referred to as λ which equals 1/β.
If μ = 0 and β = 1 it is called the standard exponential distribution and has the equation:
f(x)=e−x for x ≥ 0.
Back to top
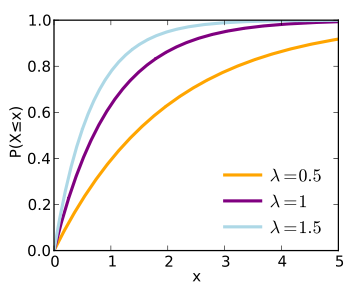
Cumulative Distribution Function
The formula for the cumulative distribution function of the exponential distribution is:
F(x) = 1 − e − λx
x ≥ 0; λ > 0
Connection to Other Distributions
The exponential distribution is related to the Poisson distribution. While the exponential models time between successive events over a continuous time interval, the Poisson distribution deals with events that happen over a fixed period of time. The number of times the event will happen within a certain amount of time is a Poisson distribution if:
- The event can happen more than one time.
- If the time elapsed between two events is exponentially distributed.
- The events are independent of previous events.
Using this definition, some natural events can fit the model. For example, the number of hurricanes that hit Hawaii each year is a Poisson distribution. However, figuring out when a machine might fail is not (as the event can only happen once).
The exponential is a special case of the gamma distribution [2]. It is the continuous counterpart of the geometric distribution, which models time between successes in a series of independent trials.
The exponential distribution is also a special case of the Weibull distribution, which happens when the Weibull shape parameter = 1.
Back to top
Exponential Family
The exponential distribution is one member of a very large class of probability distributions called the exponential families, or exponential classes. Some of the more well-known members of this family include:
- The Bernoulli distribution,
- The beta distribution,
- The binomial distribution (for a fixed number of trials),
- The Categorical distribution,
- The Chi-squared distribution,
- The Dirichlet distribution,
- The gamma distribution,
- The Geometric distribution,
- The inverse Gaussian distribution,
- The lognormal distribution.
- The negative binomial distribution (for a fixed number of failures),
- The normal distribution,
- Poisson distribution
- The von-Mises distribution,
- The von-Mises Fisher distribution.
This vast variety of distributions are connected in that they all have the following general form for their density (relative to their parameter vector, η):
Where:
- η = the parameter vector,
- h(x) & T(x) = functions — T(X) is the sufficient statistic,
- A(η) = the cumulant generating function.
Back to top
A Darmois-Koopman distribution is an exponential-type distribution. The distribution remains relatively obscure, although it has made relatively recent appearances in estimation theory.
Related Articles
- Exponential growth and decay (CalculusHowTo.com)
- Exponential Sequence (CalculusHowTo.com)
References
[1] Engineering Statistics Handbook (n.d.). Exponential Dist. Retrieved October 22, 2017 from: http://www.itl.nist.gov/div898/handbook/eda/section3/eda3667.htm.
[2] Balakrishnan, K. (1996). Exponential Dist: Theory, Methods and Applications. CRC Press.
Young & Young (1998). Statistical Ecology. Springer Science and Business Media.