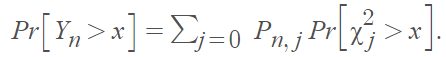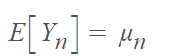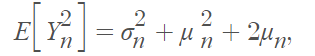Investigating a hypothesis with linear inequality constraints on the means of normal distributions? With known variances, look no further: the chi-bar-squared distribution is your best bet—a mix of different Chi Square distributions across their degrees of freedom. An ideal test statistic for such an analysis is -2 log A which has an asymptotic normal distribution when increasing populations [1][2].
If {Pn} is a sequence of probability distributions with:
- nonnegative integer support
- finite, nonzero, mean/variance
- A survival function [3]
Where:
- Yn is the random variable associated with Pn.
- pn = pn (j).
Properties
Expected value:
and
Variance
Practical Use
While chi-bar-square distributions occur frequently, calculating the weights can be an arduous task. Numerous authors have tried to solve this issue, yet it continues to remain a challenging problem with intractability being its defining characteristic. On the other hand, if you are able to make use of normal approximation then there is no need for computing every coefficient; all that is required in such case would be knowledge regarding mean and variance of universe distribution [1].
References
[1] Dykstra R 1991 Asymptotic normality for chi-bar-square distributions Can. J. Stat. 19 297–306
[2] Barlow, R. E., Bartholomew, D. J., Bremner, J. M., and Brunk, H. D. (1972). Statistical Inference under Order Restrictions, New York: Wiley.
[3] Johnson, Kotz, and Balakrishnan, (1994), Continuous Univariate Distributions, Volumes I and II, 2nd. Ed., John Wiley and Sons.