The Irwin-Hall distribution (Uniform Sum Distribution) is the distribution of the sum of n values taken from the uniform distribution U(0, 1). It is similar to the Bates distribution, which is the distribution of the mean of n values. The distribution is named after two proofs, given by Irwin (1927) and Hall (1927).
This distribution has many applications in applied mathematics, in part because of its simplicity. For example, sums of random variables need to be calculated in problems dealing with:
- Aggregating scaled values with varying significant figures,
- Change point analysis,
- Data drawn from measurements with different levels of precision (Batsyn & Kalyagin, 2012).
For small n, the distribution is very simple and follows a uniform distribution (n = 1) or triangular distribution (n = 2). It can give spline approximations to normal distributions (Marengo, 2017).
PDF of the Irwin-Hall Distribution
The probability density function (PDF) of the Irwin-Hall distribution is given by (Florescu, 2014):
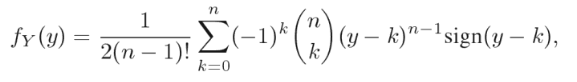
Where sign(x) is the sign function.
Mean, Variance and Kurtosis
The mean of the Irwin-Hall distribution is n / 2 and the variance is n / 12. Irwin-Hall distributions are platykurtic; For large n, the kurtosis is near to 3 (Marengo, 2017).
References
Batsyn, M. & Kalyagin, V. (2012). An Analytical Expression for the Distribution of the Sum of Random Variables with a Mixed Uniform Density and Mass Function.
Florescu, I. (2014). Probability and Stochastic Processes 1st Edition. Wiley.
Flury, B. A First Course in Multivariate Statistics (Springer Texts in Statistics) 1997 Edition.
Hall, P. (1927). The distribution of means for samples of size n drawn from a population in which
the variate takes values between 0 and 1, all such values being equally probable. Biometrika,
Vol. 19, No. 3/4. pp. 240–245.Irwin J.(1927). On the frequency distribution of the means of samples from a population having any law of frequency with finite moments, with special reference to Pearson’s type II.
Biometrika, Vol. 19, No. 3/4. pp. 225–239.
Marengo, J et al. (2017). A Geometric Derivation of the Irwin-Hall Distribution. International Journal of Mathematics and Mathematical Sciences.