Cramp Function Distribution Definition
The (complex) cramp function distribution is a continuous distribution defined as [1]:
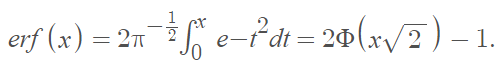
The function integrates the normal distribution, giving the probability a normally distributed random variable Y (with mean 0 and variance ½), falls into the range [−x, x].
Cramp Function vs. Error Function
The term “(complex) cramp function” is seen in literature by Russian or Latvian authors (for example, see [2], [3], [4]), where it is usually denoted as W(x) [5]. Elsewhere, it is known as the error function.
References
[1] Johnson, Kotz, and Balakrishnan, (1994), Continuous Univariate Distributions, Volumes I and II, 2nd. Ed., John Wiley and Sons.
[2] Mikhailovskiy, A. B. (1975), Theory of Plasma Instabilities, Atomizdat, in Russian
[3] Baumjohann, W., and R. A. Treumann (1997), Basic Space Plasma Physics, Imperial College Press, London.
[4] [4] Zagursky, V. Pilot signal detection in Wireless Sensor Networks (Latvian translation). Online: https://ortus.rtu.lv/science/en/publications/11860/fulltext
[5] Error Functions (TeX). Online: http://nlpc.stanford.edu/nleht/Science/reference/tex/errorfun/errorfun.tex