You may want to read this article first:
Discrete vs. Continuous Variables.
What is a Continuous Probability Distribution?
Probability distributions are either continuous probability distributions or discrete probability distributions. A continuous distribution has a range of values that are infinite, and therefore uncountable. For example, time is infinite: you could count from 0 seconds to a billion seconds…a trillion seconds…and so on, forever. A discrete distribution has a range of values that are countable. For example, the numbers on birthday cards have a possible range from 0 to 122 (122 is the age of Jeanne Calment the oldest person who ever lived).
Discrete vs. Continuous Probability Distributions
A discrete probability distribution is made up of discrete variables, while a continuous probability distribution is made up of continuous variables. The two types of distributions differ in several other ways.
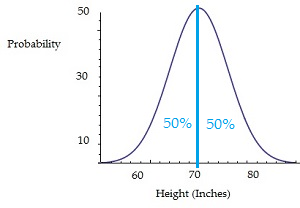
- The probability that a particular random variable will equal a certain value is zero.Delving into the fascinating realm of probability, we encounter the concept of random variables featuring continuous probability distributions, such as men’s heights. Envision a graph illustrating the distribution where the average height, precisely 70 inches, lies in the middle, evenly dividing the curve’s overarching area.
However, the probability of encountering an individual standing at an exact or fixed height of 70 inches remains an elusive, extraordinary idea. The intricate nature of continuous measurements presents boundless possibilities – our hypothetical subject could potentially be 70.1 inches tall or measure a mere 69.97 inches. Ultimately, pinpointing the precise probability of a singular fixed measurement within continuous distributions remains a beautifully enigmatic challenge.
- With continuous distributions, elegance is captured in the form of a mathematical equation known as the Probability Density Function. This formula unveils the intricate contours of the distribution’s shape. On the other hand, discrete probability distributions manifest themselves through visually appealing formats such as frequency distribution tables, graphs, and charts. To illustrate, let’s journey into the realm of rolling a six-sided die. In this mystical world, every die face possesses an equal opportunity of emerging victorious (precisely 1 out of the 6 possibilities).
Types of Continuous Probability Distribution
The normal distribution can be used the approximate the binomial distribution, as well as the hypergeometric distribution and Poisson distribution.
Other common distributions include:
- Beta distribution,
- Cauchy distribution,
- Exponential distribution,
- Gamma distribution,
- Logistic distribution,
- Weibull distribution.
Less common continuous distributions — ones you’ll rarely encounter in basic statistics courses— include:
- The Shakil-Singh-Kibria distribution, based on the Whittaker functions [1].
- Edgeworth series distribution (ESD), which approximates a probability distribution in terms of cumulants and Hermite polynomials.
References
[1] Shakil, M. et al. (2010). On a family of product distributions based on the whittaker functions and generalized pearson differential equation. Pakistan Journal of Statistics 26(1).