Probability Distributions > Folded Normal Distribution
What is a Folded Normal Distribution?
A folded normal distribution is a distribution of the absolute values of a normal distribution. It is used when you’re only interested in the size of a random variable (i.e. 2 standard deviations away from the mean) and not the direction or sign (either positive or negative). This happens in many practical situations where only the magnitude of a random variable is recorded.
It’s called a “folded” normal distribution because, quite literally, the probability mass values on the left half of the distribution have been folded over to the right half; the absolute values are taken from the left half and added to the right half.
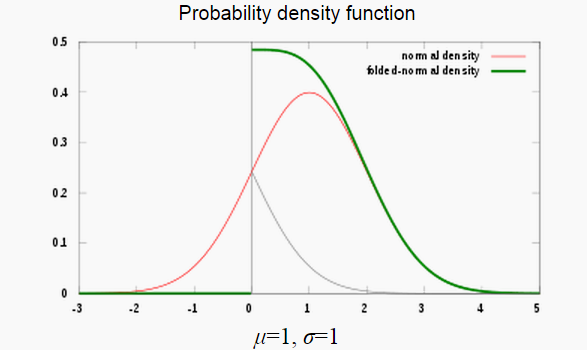
The mean( μ) and variance (σ2) of X in the original normal distribution becomes the location parameter (μ) and scale parameter (σ) of Y in the folded distribution. A more formal definition uses these two facts:
If Y is a normally distributed random variable with mean μ (the location parameter) and variance σ2 (the scale parameter), that is, if Y ∼ N μ,σ2, then the random variable X = |Y | has a folded normal distribution.
The Half-Normal Distribution
When μ = 0, and the scale parameter (σ) is 1, it is a special case of the distribution of Y called a half-normal distribution. In this distribution, x-values will always be greater or equal to zero (with a maximum value of infinity). This is one of the most important variations of the folded normal, because you’re more likely to be interested in normal distributions with a mean of 0 (i.e. a standard normal). For example, the half-normal distribution models Brownian motion — the random movement of microscopic particles suspended in a liquid or gas.
Folded Normal Distribution Calculator
This calculator on the University of Alabama in Huntsville website allows you to create a CDF of the folded normal distribution and change the parameters of the function. You can also calculate the median and the first and third quartiles. To use the calculator, select “folded normal distribution” from the drop down menu and set the view to CDF.
References
:
Ahsanullah, M; Kibria, B M G; Shakil, M. Normal and Student’s t Distributions and Their Applications. 2014.