Probability Distributions > Triangular Distribution
What is a Triangular Distribution?
A triangular distribution (sometimes called a triangle distribution) is a continuous probability distribution shaped like a triangle. It is defined by:
- a: the minimum value, where a ≤ c,
- c: the peak value (the height of the triangle), where a ≤ c ≤ b,
- b: the maximum value, where b ≥ c.
This makes it very easy to estimate the distribution’s parameters from sample data:
- Use the sample minimum as an estimator for a,
- Use the sample maximum as an estimator for b, and
- Use any reasonable statistic (e.g. the sample mean, mode or median) as an estimator for c.
If you don’t have sample data, expert knowledge can be used to estimate a probable minimum, maximum and most likely value (i.e. the mode).
The three parameters, a b and c change the shape of the triangle:
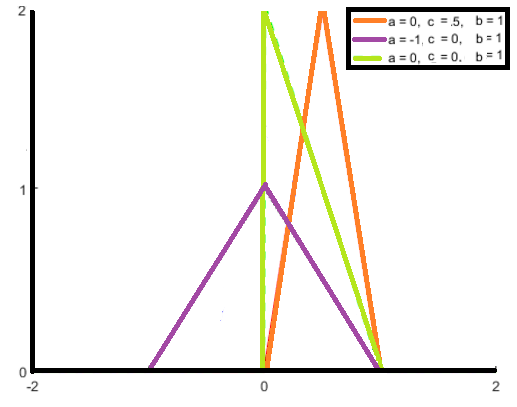
Like all probability distributions, the area under the curve is 1. Therefore, the wider the distance between a and c (i.e. the range ), the shorter the height.
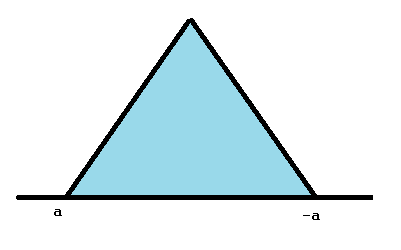
When the peak is centered at zero and a = b, it is called a symmetric triangular distribution. When this happens, a and b are equal but opposite in sign (e.g. -2, 2) and are sometimes referred to as -a and a instead of a and b.
PDF, Mean and Standard Deviation
The probability density function, which is used to find the probability a random variable falls into a certain range, is given by:
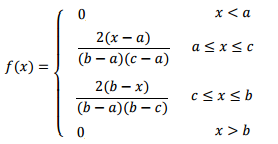
The mean for this distribution is:
μ = 1/3 (a + b + c).
The standard deviation, s, is:
s = (1/√6) a.
This formula makes the assumption that the distribution is centered at zero and that the endpoints are known.
Reference:
Samuel Kotz, S and van Dorp.J. (2004) Beyond Beta. Sample chapter on the Triangle Distribution available here from World Scientific.