The exponential power distribution is a generalization of the normal distribution. Therefore, it’s also known as the generalized normal distribution. Other names include the General Error Distribution and the Generalized Power Distribution.
PDF of the Exponential Power Distribution
The Probability Density Function (PDF) of the Exponential Power Distribution is:
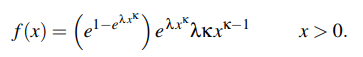
Where:
- λ = positive scale parameter,
- κ = positive shape parameter.
The extra parameter allows the distribution to represent many more distributional shapes. It also allows more flexibility with kurtosis, which can be represented by a variety of values (rather than just a constant).
Advantages and Disadvantages
As well as the extra parameter, which allows more flexibility with distributional shapes and kurtosis. However, a “major drawback” is that the distribution doesn’t allow for asymmetrical data (Konunjer, n.d.). However, it is possible to derive a slightly different model with skew (e.g. the skew exponential power model proposed by Ayebo and Kozubowski).
Other features include:
- Heavy tails,
- Symmetry around the mean,
- Unimodality,
- Bathtub shaped hazard function,
References
Ayebo, A. and Kozubowski, T. An asymmetric generalization of Gaussian and Laplace laws. Retrieved Auhust 12, 2019 from: https://wolfweb.unr.edu/homepage/tkozubow/0skeexp1.pdf
Package Normalp. Retrieved August 12, 2019 from: https://cran.case.edu/web/packages/normalp/normalp.pdf
Exponential Power. Retrieved August 12, 2019 from: http://www.math.wm.edu/~leemis/chart/UDR/PDFs/Exponentialpower.pdf
Konunjer, I. Asymmetric Power Distribution: Theory and Applications to Risk Measurement.
Kotchlamazashvili, Z. (2014). Empirical Analysis of the EU Term Structure of Interest Rates. Logos Verlag Berlin GmbH.