The term “Eulerian distribution” may refer to:
- A distribution used in permutation statistics to count descents, or
- A Type III (p/q, p) distribution.
Eulerian Distribution in Permutation Statistics
In permutation statistics, the Eulerian distribution is the classical name for the distribution of the descent statistics. A descent in a permutation α1, α2, …, αn is an index I for which αi > αi+1 [1]. The Eulerian number counts the number of permutations in a descent set with exactly k descents [2].
Type III (p/q, p) Eulerian Distribution
The term Eulerian distribution may also refer to a Type III (p/q, p) distribution [3]. Kendall’s 1948 Biometrika article, titled “On some modes of population growth leading to R.A. Fisher’s logarithmic series distribution,” concerns relative numbers of animals from different species obtained when random sampling from a heterogeneous population. Fisher assumed that for a certain species, the number of individuals caught in a specific time would be distributed as a Poisson variable with expectation ωt, where ω is the “intrinsic abundance”. The following formula, describing the distribution of ω, is referenced as a Eulerian (or χ2) form:
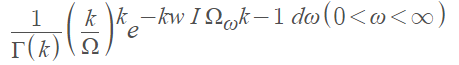
Where
- Ω is the mean value of ω.
- k is a constant parameter.
References
[1] Mansour, T. & Munagi, A. (2010). Enumeration of partitions by rises, levels, and descent. In Permutation Patterns. Cambridge University Press.
[2] Hibi & Tsuchiya. (2019). Algebraic And Geometric Combinatorics On Lattice Polytopes – Proceedings Of The Summer Workshop On Lattice Polytopes. World Scientific.
[3] Kendall, D. G. (1948). On Some Modes of Population Growth Leading to R. A. Fisher’s Logarithmic Series Distribution. Biometrika, 35(1/2), 6–15. https://doi.org/10.2307/2332624