Probability distributions > Beta prime distribution
With its fat tails decreasing polynomially, the Beta Prime Distribution is a continuous probability distribution that can be used to study Bayesian statistics. This important family of prior distributions offers valuable insight in exploring how certain factors influence outcomes on binomial experiments.
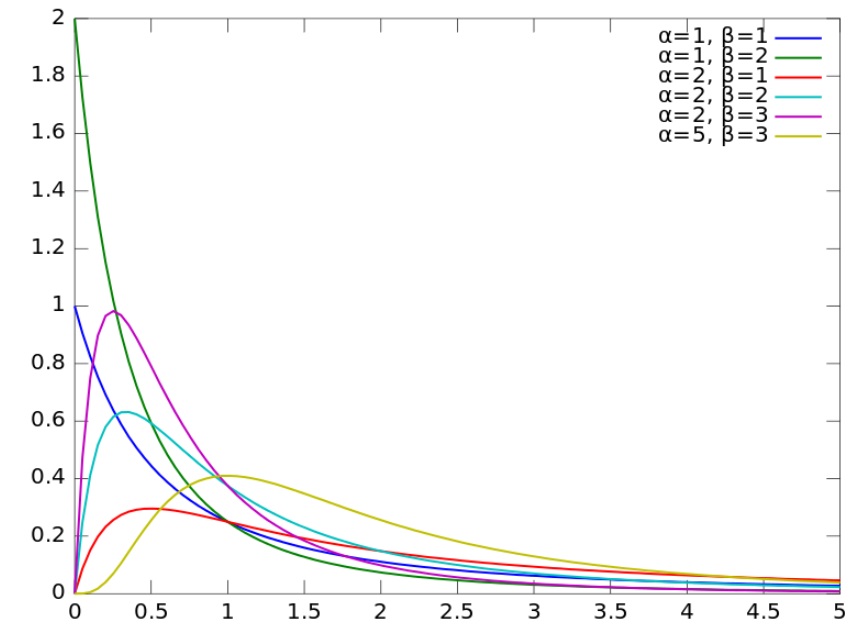
The beta distribution is versatile, with a range of aliases like compound gamma, Pearson type VI and variance ratio. It’s closely related to the beta prime distribution; if you want to calculate from one – just minus 1 from your value for Z before working out X [2].
The standardized probability density function:
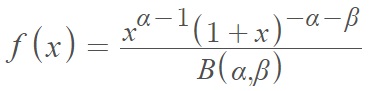
Where:
- α and β = non-negative shape parameters
- Β(α, β) = the beta function.
The cumulative distribution function = F(x) = Ix/(1+x)(α, β).
The mean = α(β – 1) for β > 1.
The mode = (α – 1)/ (α + β – 2) for α > 1, β > 1.
The median = DNE.
Special Cases
The beta prime distribution is a powerful tool when studying probability distributions, with many special cases intersecting at its boundaries. Notable examples include the Burr and Dagum Distributions as well as the Log-Logistic Distribution – all particular applications of this versatile model.
References
Laurent, S. (2019). R-Bloggers–The Beta Distribution of the Third Kind. Retrieved December 31, 2021 from: https://www.r-bloggers.com/2019/07/the-beta-distribution-of-the-third-kind-or-generalised-beta-prime/