Probability Distributions > Gompertz Distribution
What is the Gompertz Distribution?
The Gompertz distribution, named after Benjamin Gompertz, is an exponentially increasing, continuous probability distribution. It’s basically a truncated extreme value distribution (Johnson et. al, 1994). Therefore, it is also called an EVD Type I. Although the theoretical range is from zero to positive infinity, most applications for this distribution are for human mortality rates with a range of 0 to ≅ 100. It is also used in other fields, including biology and demography.
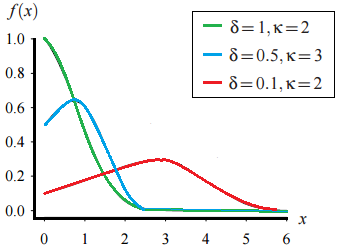
Probability Density Function
Two shape parameters, δ and κ control the shape of the probability density function.
Formal definition
The Gompertz can be defined by the following differential equation (Marshall & Olkin, 2007):
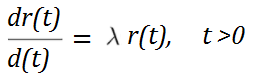
Where:
- r(t) is the hazard rate
When λ = 1, this becomes the exponential distribution.
Gompertz supposed that the hazard rate was your chances of death at time t. He concluded that this rate increased in geometrical progression:
![]()
When λ and ξ are both less than zero, this becomes the negative Gompertz distribution.
Relation to Other Distributions
The Gompertz is related to:
- The extreme value distribution: If X has the standard extreme value distribution for minimums, then the conditional distribution of X (given X ≥ 0 ) is a standard Gompertz.
- The exponential distribution: The exponential distribution is made up of limits of sequences of Gompertz distributions (Marshall & Olkin, 2007). Put more simply, a series of exponential distributions can be combined to make a Gompertz. If X has a basic Gompertz dist. (with shape parameter a), then Y = eX − 1 has an exponential distribution with rate parameter a.
- The Gompertz is a log-Weibull distribution This is because the log of the hazard rate is linear in t, giving: λ(t) = exp{α + Βt). The log of the hazard rate in the Weibull is also linear in t (Rodriguez).
Other Forms
Various forms of the Gompertz exist, in part because of its long history. It was first developed by Benjamin Gompertz in 1825, as a way to model age-specific mortality rates. Although it was used widely in Victorian times, the Gompertz “law” lost popularity at the turn of the 20th century but is recently regaining ground in several different forms, which include:
- The generalized Gompertz with three parameters, introduced by El-Gohary et al. (2013).
- The beta-Gompertz, introduced by Ali et al. (2014), is a generalized version with four parameters.
- The negative Gompertz distribution has an additional negative rate of aging parameter.
- The generalized Gompertz distribution (GGD) differs from the “regular” distribution in that “it has increasing or constant or decreasing or bathtub curve failure rate depending upon the shape parameter” (El-Gohary et. al).
- The Exponentiated Generalized Weibull-Gompertz Distribution generalizes several distributions, including the Gompertz.
References:
El-Gohary, A et. al. (2013). The generalized Gompertz distribution. Applied Mathematical Modelling. Volume 37, Issues 1–2, January 2013, Pages 13–24
Johnson, N.L., Kotz, S., and Balakrishnan, N. (1994), Continuous Univariate Distributions (Vol. I, 2nd ed.), New York: Wiley.
Marshall & Olkin (2007. Life Distributions: Structure of Nonparametric, Semiparametric, and Parametric Families. Springer Science & Business Media.
Rodriguez, G. Parametric Survival Models. Available here.