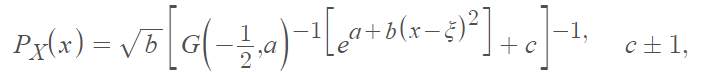Ferreri distributions (distribuzione di Ferreri) are a system of probability distributions described by Ferreri. The distributions have probability density functions (PDFs) is a four-parameter distribution of the form [1]:
where
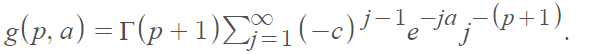
(a, b, c, ξ) are the four parameters: ξ is the mean.
- If c = 1, β2 < 3;
- If c = – 1, β2 > 3.
- As a increases, the distribution approaches a normal distribution [2].
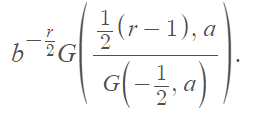
While the distribution is usually attributed to Ferreri (1964), there is a mention of the “Ferreri distribution” in the 1959 book International Journal of Abstracts: Statistical Theory and Methods Volume 1 [3]

Due to the age of the source material, I was unable to obtain any originals to confirm more details about the distribution or its origins (Note: Brown University [4] has one copy in offsite storage). Outside of entries in various dictionaries – such as the Oxford Dictionary of Statistical Terms [5] –there is a general dearth of entries about the Ferreri distributions in the literature. This appears to be one of those distributions that is destined to vanish into obscurity.
References
[1] Ferreri, C. (1964). A new frequency distribution for single variate analysis, Statistica (Bologna), 24, 223-251. (In Italian)
[2] Johnson, Kotz, and Balakrishnan, (1994), Continuous Univariate Distributions, Volumes I and II, 2nd. Ed., John Wiley and Sons.
[3] JOURNAL International journal of abstracts, statistical theory and method. Edinburgh : Published for the International Statistical Institute by Oliver and Boyd/ Vol. 1, no. 1 (July 1959)-v. 4, no. 4. c1959-c1963
[4] Dodge, Y. et al. (Eds.). (2006). The Oxford Dictionary of Statistical Terms. Oxford University Press.
[5] JOURNAL Entry https://bruknow.library.brown.edu/discovery/fulldisplay/alma991020951269706966/01BU_INST:BROWN