Statistics Definitions > Hypergeometric Distribution
Contents:
- What is the Hypergeometric Distribution?
- Application of Hypergeometric Distribution in Real Life: Examples
What is the Hypergeometric Distribution?
The hypergeometric distribution is a probability distribution that’s very similar to the binomial distribution. In fact, the binomial distribution is a very good approximation of the hypergeometric distribution as long as you are sampling 5% or less of the population.
Therefore, in order to understand the hypergeometric distribution, you should be very familiar with the binomial distribution. Plus, you should be fairly comfortable with the combinations formula.
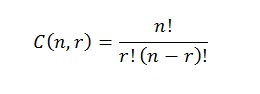
If you need a brush up, see:
Hypergeometric Distribution Formula
Watch the video for an example:
The (somewhat formal) definition for the hypergeometric distribution, where X is a random variable, is:
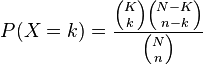
Where:
- K is the number of successes in the population
- k is the number of observed successes
- N is the population size
- n is the number of draws
You could just plug your values into the formula. However, if formulas aren’t your thing, another way is just to think through the problem, using your knowledge of combinations.
Hypergeometric Distribution Example 1
A deck of cards contains 20 cards: 6 red cards and 14 black cards. 5 cards are drawn randomly without replacement. What is the probability that exactly 4 red cards are drawn?
The probability of choosing exactly 4 red cards is:
P(4 red cards) = # samples with 4 red cards and 1 black card / # of possible 4 card samples
Using the combinations formula, the problem becomes:
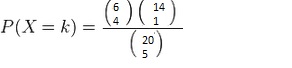
In shorthand, the above formula can be written as:
(6C4*14C1)/20C5
where
- 6C4 means that out of 6 possible red cards, we are choosing 4.
- 14C1 means that out of a possible 14 black cards, we’re choosing 1.
Solution = (6C4*14C1)/20C5 = 15*14/15504 = 0.0135
The binomial distribution doesn’t apply here, because the cards are not replaced once they are drawn. In other words, the trials are not independent events. For example, for 1 red card, the probability is 6/20 on the first draw. If that card is red, the probability of choosing another red card falls to 5/19.
Hypergeometric Distribution Example 2
A small voting district has 101 female voters and 95 male voters. A random sample of 10 voters is drawn. What is the probability exactly 7 of the voters will be female?
101C7*95C3/(196C10)= (17199613200*138415)/18257282924056176 = 0.130
Where:
- 101C7 is the number of ways of choosing 7 females from 101 and
- 95C3 is the number of ways of choosing 3 male voters* from 95
- 196C10 is the total voters (196) of which we are choosing 10
*That’s because if 7/10 voters are female, then 3/10 voters must be male.
Check out our YouTube channel for hundreds of statistics help videos!
Application of Hypergeometric Distribution in Real Life: Examples
The hypergeometric distribution describes the number of successes in a sequence of n trials from a finite population without replacement. At first glance, it might seem that this is a purely academic distribution, but there are actually many different applications of the hypergeometric distribution in real life.

One of the most common applications of the hypergeometric distribution is in industrial quality control, such as calculating probabilities for defective parts produced in a factory. Let’s say a factory line produces 1% defective parts that are boxed at the end of the line; The hypergeometric distribution can be used to model the occurrence of defective parts for quality control purposes, as long as the items being sampled from a box are not replaced.
In electrochemistry, the hypergeometric distribution can predict the effect of surface deterioration on electrode behavior for any electrode process with two competing reactions. This gives valuable information about the effectiveness of electrode-electrolyte interfaces and improves interpretation of the measurements of surface properties [1].
If you play poker, the hypergeometric distribution can tell you the probability of getting 3 of the same suit in a 5 card hand (or any number of other card/hand combinations).
The PowerBall lottery game is a televised, two part drawing. In the first stage, five white balls are drawn randomly from a bowl of 49 balls. In the second stage, one red ball (the PowerBall) is drawn randomly from a bowl of 42 balls. The probability of success changes from one draw to the next (the balls are not replaced), so the probabilities for the game can be modeled with the hypergeometric distribution [2].
References
[1] Fahidy, T. (2012). An application of hypergeometric distribution theory to competitive processes at deteriorating electrode surfaces. In Electrochemistry Communications, 282-284.
[2] Anderson, J. & Schmidt, J. (2002). Playing Powerball?. Proceedings. Annual Conference on Taxation and Minutes of the Annual Meeting of the National Tax Association. pp. 377-382.
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.