The term “special distribution” doesn’t refer to a specific distribution or family of distributions, but rather any probability distribution that is given a special name. These distributions are important in statistics for many reasons: they may model a wide range of phenomena, or they may be related to other special distributions via conditioning (which means an event is treated as having occurred), limits, or transformations. You can think of these distributions as being “useful” or “important” — they generally:
- Have simple form Probability Density Functions (if they are continuous probability distributions) or Probability Mass Functions (if they are discrete probability distributions),
- Are used for a wide range of applications and uses,
- Are well known within the field they are applied to.
Special Distribution List
The following list of special distributions are widely used in probability and statistics, number theory, physics, and many other sciences:
- Arcsine distribution.
- Benford’s Law.
- Bernoulli Distribution: Definition and Examples
- Beta distribution.
- Beta prime distribution.
- Binomial Distribution.
- Cauchy distribution.
- Chi-square distribution.
- Discrete, Continuous, and General uniform distributions.
- Erlang Distribution: Definition, Examples
- Exponential distributions.
- Exponential-logarithmic distribution.
- Extreme Value Distribution.
- F-distribution.
- Folded normal distribution.
- Gamma distribution.
- Geometric Distribution.
- Gompertz distribution.
- Hyperbolic secant distribution.
- Irwin-Hall distribution.
- Laplace distribution.
- Lévy distribution.
- Location scale distribution.
- Logarithmic distribution.
- Logistic distribution.
- Log-logistic distribution.
- Lognormal distribution.
- Maxwell-Boltzmann distribution.
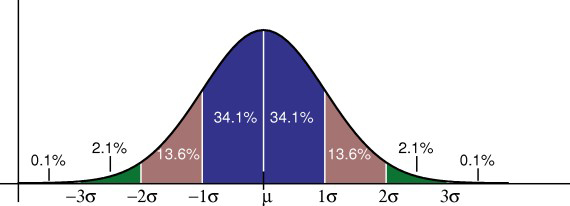
- Normal distributions.
- Pareto distribution.
- Power series distribution.
- Rayleigh distribution.
- Semicircle Distribution.
- Sine distribution.
- Stable distributions.
- Student’s t-distribution.
- Triangle distribution.
- U-power distribution.
- Wald distribution.
- Weibull distribution.
- Zeta distribution.