The Waring distribution is a generalization of the Simon-Yule distribution. To put that another way, the Simon-Yule is a special case of the Waring distribution when the parameters take on certain limiting values. The Waring has two parameters (α and β); The generalized form has an additional parameter ν.
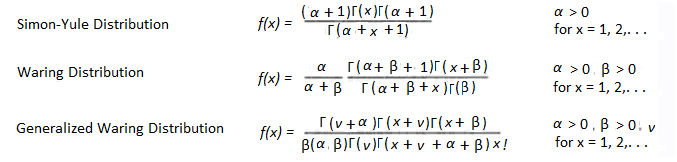
The Waring is a theoretical distribution with limited (if any) applications to real-life data. Sichel (1992, as cited in Hahn & Keeble, 1998) states that it has “…linear tails in a logarithmic grid, and hence [is] unsuitable for representing the upper tails of most observed biometric size-frequency data.” It is sometimes linked to the Pareto distribution, because the tails show Pareto-like behavior (Arnold, 2015, p. 292).
Disambiguation
The term “Waring Distribution” usually refers to a generalization of the Yule distribution, but many variants on the name exist, so it can get a little confusing. To add to the confusion, subtle changes in the generating mechanism for the Simon-Yule distribution (a.k.a. a specific form of the Waring) lead to various other distributions (e.g. the Poisson distribution). The generalized Waring distribution is sometimes called the beta negative binomial distribution.
When working with this distribution, make sure you understand the context. For example, in the Wolfram documentation, “Waring-Yule Distribution” refers to the Yule–Simon distribution:
- WaringYuleDistribution[α] represents the Yule distribution with shape parameter α.
- WaringYuleDistribution[α,β] represents the Waring with shape parameters α and β.
References
Applied Mathematics and Computation. 217 (21): 8560–8566.
Hahn, T. & Buckland, (1998). Historical Studies in Information Science. Information Today, Inc.
Hazewinkel, M. (2001). Encyclopaedia of Mathematics, Supplement III. Springer Science & Business Media.
King, M. (2017). Statistics: A Practical Approach for Process Control Engineers. John Wiley and Sons.
Wolfram language and documentation center. WaringYuleDistribution. Retrieved March 29, 2019 from: https://reference.wolfram.com/language/ref/WaringYuleDistribution.html
Yule, G. U. (1925). “A Mathematical Theory of Evolution, based on the Conclusions of Dr. J. C. Willis, F.R.S”. Philosophical Transactions of the Royal Society B. 213 (402–410): 21–87