The Muth distribution, a model for non-negative continuous random variables, was introduced by Muth in 1977 [1]. The distribution has largely been overlooked in the statistical literature [2]; the distribution isn’t usually encountered in introductory probability and statistics courses. However, you’ll come across it in reliability theory, which deals with a system’s ability to function under certain conditions (like the effect of average time to repair) for a specified time period.
PDF and Characteristics of the Muth Distribution
The shorthand X ∼ Muth(β) indicates that a random variable X has the Muth distribution with parameter β.
The probability density function for the standard Muth distribution is:
f(x; β) = e βx – β) e -(1 / β)(e βx – 1) + βx
Where β is a shape parameter.
The distribution, which is based on a limited time interval, is flexible enough to fit a wide variety of lifetime datasets. It has several other notable characteristics:
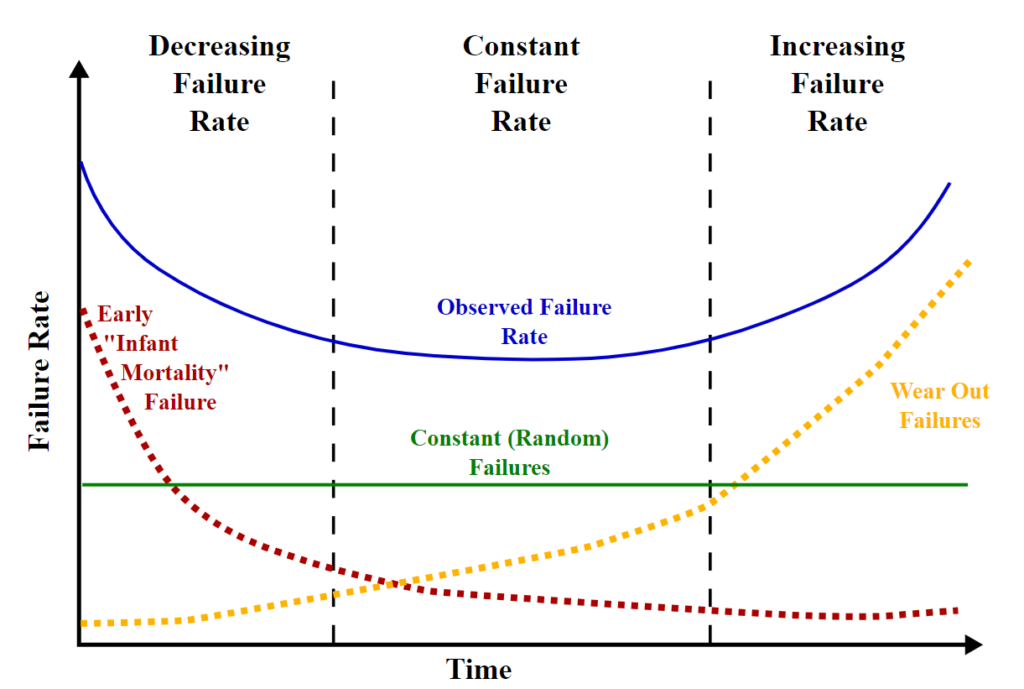
- It has the bathtub hazard function with a vertical asymptote [3].
- The distribution corresponds to the exponential distribution as β approaches zero.
- It’s tail is less weighted than other lifetime distributions like the exponential, lognormal or Weibull.
References
Bathtub_curve.jpg: Wyattsderivative work: McSush, Public domain, via Wikimedia Commons
[1] J.E. Muth. (1977). Reliability models with positive memory derived from the mean
residual life function. In C.P. Tsokos and I. Shimi (Eds.), The Theory and
Applications of Reliability, volume 2, pp. 401–435. Academic Press, Inc., New
York.
[2] Jodrá, P. & Arshad, M. (2021). An intermediate muth distribution with increasing failure rate. Communications in Statistics – Theory and Methods. Retrieved November 12, 2021 from: https://www.tandfonline.com/doi/abs/10.1080/03610926.2021.1892133?journalCode=lsta20
[3] Kosznik-Biernacka, S. (2007). Makeham’s Generalised Distribution. Computational Methods in Science and Technology 13(2), 113-120 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.552.4465&rep=rep1&type=pdf